Why does the photoelectric effect supports particle theory – Why does the photoelectric effect support particle theory? This seemingly simple question unravels a century-old scientific revolution. The photoelectric effect, the emission of electrons from a material when light shines on it, flatly contradicted classical wave theory. Classical physics predicted a gradual electron emission dependent on light intensity, a prediction spectacularly at odds with experimental observations. Einstein’s groundbreaking explanation, invoking the concept of light quanta – photons – provided the missing piece, solidifying the particle nature of light and laying the foundation for quantum mechanics.
This seemingly esoteric phenomenon has far-reaching implications, impacting everything from medical imaging to solar energy technology. We will dissect the crucial evidence and explore the political implications of this paradigm shift in physics.
The experimental setup involved shining light of varying frequencies and intensities onto a metal surface, measuring the resulting electron emission. Classical wave theory, which viewed light as a continuous wave, failed to explain the observed threshold frequency – a minimum frequency below which no electrons were emitted, regardless of intensity. Einstein’s revolutionary hypothesis posited that light energy is quantized into discrete packets called photons, each with energy proportional to its frequency (E=hf).
This elegantly explained the threshold frequency and the linear relationship between photon frequency and electron kinetic energy, decisively refuting the wave model’s predictions. The political ramifications of this shift were immense, challenging established scientific dogma and paving the way for a new era of physics. The implications of abandoning classical physics for the more accurate quantum theory had profound effects on scientific funding and research priorities.
Introduction to the Photoelectric Effect
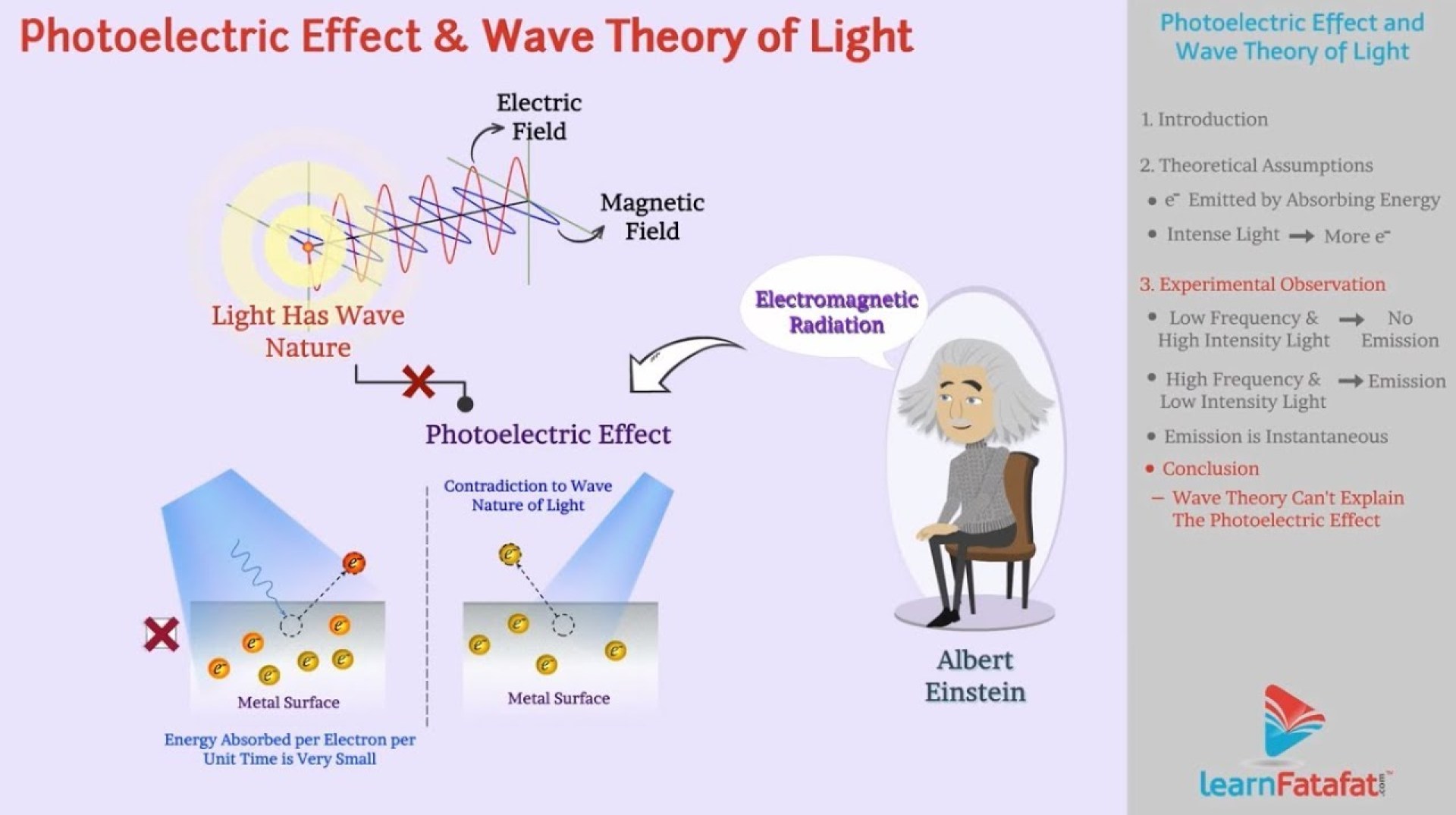
The photoelectric effect is a fascinating phenomenon that involves the emission of electrons from a material when light shines on it. This seemingly simple interaction played a crucial role in the development of quantum mechanics, challenging classical physics and ultimately supporting the particle theory of light. Understanding the experimental setup and the discrepancies between observations and classical predictions is key to appreciating its significance.The experimental setup typically involves a metal plate (the cathode) inside a vacuum tube.
Light of a specific frequency is shone onto this plate. A second plate (the anode), held at a positive potential, is placed nearby. The emitted electrons, if any, are attracted to the anode, creating a measurable electric current. By varying the intensity and frequency of the light, as well as the potential difference between the plates, scientists can study the characteristics of the emitted electrons.Electron emission is observed only when the light’s frequency exceeds a certain threshold frequency, specific to the metal used.
Below this threshold, no electrons are emitted, regardless of the light’s intensity. Above the threshold, the number of emitted electrons increases with the intensity of the light, but their maximum kinetic energy depends only on the light’s frequency, not its intensity. This was a puzzling observation.
Classical Wave Theory Prediction and its Failure
Classical wave theory, prevalent at the time, predicted that light’s energy is proportional to its intensity. A brighter light (higher intensity) should transfer more energy to the electrons in the metal, leading to electron emission even at low frequencies, given enough time. The intensity should also determine the maximum kinetic energy of the emitted electrons; higher intensity should mean higher kinetic energy.
Furthermore, there should be a time delay between the light exposure and electron emission, as the electrons would need to accumulate energy gradually. However, experimental observations directly contradicted these predictions. The existence of a threshold frequency, the independence of maximum kinetic energy from light intensity, and the lack of any time delay all pointed towards a fundamental flaw in the classical wave model’s explanation of the photoelectric effect.
These experimental results could only be successfully explained by considering light as a stream of particles, each carrying a discrete amount of energy proportional to its frequency.
Einstein’s Explanation and the Particle Nature of Light: Why Does The Photoelectric Effect Supports Particle Theory
Einstein’s explanation of the photoelectric effect revolutionized our understanding of light, shifting it from a purely wave-based phenomenon to one exhibiting particle-like properties. His work provided crucial evidence supporting the concept of light quanta, now known as photons, and laid the foundation for the development of quantum mechanics.
Einstein’s Hypothesis on Light Quanta (Photons)
Einstein proposed that light energy is not continuously distributed as waves, but rather exists as discrete packets of energy called photons. Each photon’s energy is directly proportional to its frequency. This hypothesis directly addressed the shortcomings of the classical wave theory in explaining the photoelectric effect. The wave theory couldn’t explain why the emission of electrons depended on the frequency of light, not its intensity, or why there was a threshold frequency below which no electrons were emitted, regardless of intensity.
Einstein postulated that a single photon interacts with a single electron, transferring its energy directly. This discrete energy transfer is the key to understanding the photoelectric effect. In contrast, the classical wave theory predicted a gradual energy transfer from the light wave to the electron, a prediction not supported by experimental observations.
Energy-Frequency Relationship of Photons
The relationship between a photon’s energy (E) and its frequency (f) is given by Einstein’s equation:
E = hf
where h is Planck’s constant, approximately 6.626 x 10 -34 Js. Planck’s constant represents the fundamental proportionality between energy and frequency at the quantum level. It’s a universal constant, meaning it holds true for all photons regardless of their source or type.A graph plotting energy (E) on the y-axis (in Joules) against frequency (f) on the x-axis (in Hertz) would show a linear relationship with a slope equal to Planck’s constant.Here are three examples calculating photon energies:* Visible Light: A photon of green light with a frequency of 5.5 x 10 14 Hz has an energy of E = (6.626 x 10 -34 Js)(5.5 x 10 14 Hz) ≈ 3.64 x 10 -19 J.
Ultraviolet Light
A photon of ultraviolet light with a frequency of 1.5 x 10 15 Hz has an energy of E = (6.626 x 10 -34 Js)(1.5 x 10 15 Hz) ≈ 9.94 x 10 -19 J.
X-rays
A photon of X-rays with a frequency of 3.0 x 10 18 Hz has an energy of E = (6.626 x 10 -34 Js)(3.0 x 10 18 Hz) ≈ 1.99 x 10 -15 J.
Threshold Frequency and its Significance
The threshold frequency (f 0) is the minimum frequency of light required to initiate the photoelectric effect for a given metal. If the frequency of incident light is below the threshold frequency, no electrons will be emitted, regardless of the light’s intensity. This threshold frequency is directly related to the work function (Φ) of the metal, which is the minimum energy required to remove an electron from the metal’s surface.
The relationship is given by:
Φ = hf0
The following table shows threshold frequencies and work functions for three metals:
| Metal | Work Function (Φ) (J) | Threshold Frequency (f0) (Hz) |
|---|---|---|
| Sodium | 3.65 x 10-19 | 5.5 x 1014 |
| Zinc | 6.61 x 10-19 | 1.0 x 1015 |
| Platinum | 9.0 x 10-19 | 1.4 x 1015 |
Illustrative Example
A typical photoelectric effect experiment involves shining light of varying frequencies and intensities onto a metal surface inside an evacuated chamber. The emitted electrons are collected by a positively charged electrode, creating a current. The apparatus includes a light source (with adjustable frequency and intensity), a metal plate (cathode), a collecting electrode (anode), and an ammeter to measure the current.
By varying the frequency and intensity of the light and measuring the resulting current, one can observe that the current only begins to flow above a certain threshold frequency, independent of intensity, directly supporting Einstein’s hypothesis. A diagram would show the light source aimed at the cathode, the emitted electrons traveling to the anode, and the ammeter measuring the resulting current.
The experimental results would demonstrate a linear relationship between the maximum kinetic energy of the emitted electrons and the frequency of the incident light, further confirming the photon theory.
The Role of Frequency in Electron Emission
The photoelectric effect reveals a crucial interplay between the frequency of incident light and the kinetic energy of emitted electrons. Understanding this relationship is key to demonstrating the particle nature of light and refuting classical wave theory predictions. This section delves into the specifics of this relationship, exploring how light intensity and frequency independently influence electron emission.
Light Intensity and Electron Kinetic Energy, Why does the photoelectric effect supports particle theory
Increasing the intensity of light, while keeping the frequency constant, increases the number of photons striking the metal surface. This, in turn, increases the number of electrons emitted, leading to a larger photoelectric current. However, the kinetic energy of each individual emitted electron remains unchanged. This is because the kinetic energy of a single emitted electron depends solely on the energy of the individual photon striking it, which is determined by the light’s frequency, not its intensity.
A more intense light simply means more photons of the same energy are hitting the surface.The relevant equation is Einstein’s photoelectric equation:
KEmax = hf – Φ
where KE max is the maximum kinetic energy of the emitted electrons, h is Planck’s constant, f is the frequency of the incident light, and Φ is the work function of the metal (the minimum energy required to remove an electron from the metal’s surface). Notice that intensity is not a factor in this equation.A graph illustrating this would show a horizontal line representing KE max remaining constant as light intensity increases along the x-axis.
The y-axis would represent the maximum kinetic energy of the emitted electrons.
Light Frequency and Electron Kinetic Energy
Increasing the frequency of the incident light directly increases the energy of each individual photon (E = hf). This, according to Einstein’s equation (KE max = hf – Φ), leads to a directly proportional increase in the maximum kinetic energy of the emitted electrons.The threshold frequency (f 0) is the minimum frequency of light required to initiate electron emission.
Below this frequency, even with high intensity, no electrons are emitted because the energy of individual photons is insufficient to overcome the work function (hf < Φ). Above the threshold frequency (hf > Φ), electrons are emitted, and their maximum kinetic energy increases linearly with the frequency of the incident light.A graph showing this relationship would have frequency (f) on the x-axis and maximum kinetic energy (KEmax) on the y-axis. The line would start at the x-intercept, representing the threshold frequency (f 0), and increase linearly with a slope equal to Planck’s constant (h). The y-intercept would represent -Φ.
Particle vs. Wave Theory Predictions
Classical wave theory predicted that increasing light intensity (amplitude) should increase the kinetic energy of emitted electrons, regardless of frequency. It also predicted a time delay before electron emission, as the wave would need to accumulate enough energy to eject an electron. The wave theory failed to predict a threshold frequency.In contrast, the particle theory (photon theory) accurately predicts the existence of a threshold frequency, the linear relationship between frequency and kinetic energy above the threshold, and the instantaneous nature of electron emission.
Each photon interacts with a single electron, transferring its energy directly. If the photon’s energy is below the work function, no emission occurs, regardless of intensity.
Experimental Verification
A simple experiment to demonstrate this relationship could use a photoelectric effect apparatus consisting of a light source with adjustable frequency (e.g., a monochromatic light source with filters), a metal plate (cathode), a collecting electrode (anode), and a voltmeter and ammeter to measure the stopping potential (related to KE max) and photoelectric current, respectively.The procedure would involve shining light of different frequencies onto the cathode and measuring the stopping potential (V s) for each frequency.
The maximum kinetic energy can be calculated using KE max = eV s, where e is the elementary charge. The data would be plotted as a graph of stopping potential (or KE max) versus frequency. A linear relationship would confirm the particle theory.A sample data table might look like this:
| Frequency (Hz) | Stopping Potential (V) | KEmax (eV) |
|---|---|---|
| 5 x 1014 | 0.5 | 0.5 |
| 6 x 1014 | 1.0 | 1.0 |
| 7 x 1014 | 1.5 | 1.5 |
Further Considerations
The simple model presented has limitations. The work function (Φ) varies for different materials, and temperature can affect electron emission. More sophisticated models incorporate these factors for a more accurate description of the photoelectric effect.
Kinetic Energy of Emitted Electrons
The kinetic energy of emitted electrons in the photoelectric effect is a crucial piece of evidence supporting the particle nature of light. Understanding this energy helps us solidify the connection between light’s frequency and the energy of emitted electrons, ultimately refuting the predictions of classical wave theory.
Formula Derivation and Application
The relationship between photon energy, work function, and the maximum kinetic energy of emitted electrons is elegantly described by the equation derived from the conservation of energy. When a photon strikes a metal surface, its energy is transferred to an electron. If this energy exceeds the work function of the metal, the electron is ejected with a certain kinetic energy.
Ephoton = Φ + K max
where:* E photon = energy of the incident photon (hν, where h is Planck’s constant and ν is the frequency of light)
- Φ = work function of the metal (the minimum energy required to remove an electron from the metal’s surface)
- K max = maximum kinetic energy of the emitted electron
This equation is derived directly from the principle of conservation of energy. The energy of the incoming photon is completely transformed into two components: the energy required to overcome the binding forces holding the electron within the metal (the work function), and the remaining energy that becomes the kinetic energy of the ejected electron.Here are three example problems illustrating the application of this formula: Problem 1: A photon with a frequency of 1.0 x 10 15 Hz strikes a sodium surface (Φ = 2.3 eV).
Yo, so the photoelectric effect, right? It’s all about how light knocks electrons loose, which totally screams “particle,” not wave. Think about it – predicting that kinda behavior needs a particle model, not some wavy-gravy stuff. It’s like, check this out if you wanna dig deeper into unpredictable futures: is critical theory accept the future is unkwonw – kinda related, right?
Anyway, back to the photoelectric effect: the energy of the ejected electrons directly depends on the light’s frequency, another solid particle clue. It’s mad science, fam.
What is the maximum kinetic energy of the emitted electrons? (h = 6.63 x 10 -34 Js, 1 eV = 1.6 x 10 -19 J) Solution:E photon = hν = (6.63 x 10 -34 Js)(1.0 x 10 15 Hz) = 6.63 x 10 -19 J = 4.14 eVK max = E photon
Φ = 4.14 eV – 2.3 eV = 1.84 eV
Problem 2: A photon with an energy of 5.0 eV strikes a copper surface (Φ = 4.7 eV). Will electrons be emitted? If so, what is their maximum kinetic energy? Solution: Since the photon energy (5.0 eV) is less than the work function of copper (4.7 eV), no electrons will be emitted. Problem 3: Electrons are emitted from a zinc surface (Φ = 4.3 eV) with a maximum kinetic energy of 1.5 eV.
What is the frequency of the incident photons? Solution:E photon = K max + Φ = 1.5 eV + 4.3 eV = 5.8 eV = 9.28 x 10 -19 Jν = E photon / h = (9.28 x 10 -19 J) / (6.63 x 10 -34 Js) = 1.4 x 10 15 Hz
Work Function Exploration
The work function (Φ) represents the minimum energy needed to liberate an electron from a metal’s surface. It’s determined by the material’s properties, including its crystal structure, atomic arrangement, and the strength of the bonds holding electrons to the atoms. A higher work function indicates that electrons are more tightly bound to the metal, requiring more energy to be ejected.The following table lists the work functions of five different metals:
| Metal | Work Function (eV) | Source |
|---|---|---|
| Sodium (Na) | 2.3 | CRC Handbook of Chemistry and Physics |
| Copper (Cu) | 4.7 | CRC Handbook of Chemistry and Physics |
| Zinc (Zn) | 4.3 | CRC Handbook of Chemistry and Physics |
| Aluminum (Al) | 4.2 | CRC Handbook of Chemistry and Physics |
| Gold (Au) | 5.1 | CRC Handbook of Chemistry and Physics |
A higher work function implies a higher threshold frequency (ν 0) of incident light needed to initiate electron emission. The threshold frequency is the minimum frequency at which the photon energy (hν 0) equals the work function (Φ): hν 0 = Φ.
Particle Theory Explanation
The particle theory of light, also known as the photon theory, elegantly explains the observed features of the photoelectric effect. The maximum kinetic energy of emitted electrons is directly proportional to the frequency of the incident light (K max ∝ ν) but independent of the light intensity. This is because each photon interacts with a single electron, transferring its energy directly.
Increasing the intensity increases the number of photons, hence the number of emitted electrons, but doesn’t change the energy of each individual photon.Electrons are only emitted above a certain threshold frequency because the photon’s energy must exceed the work function of the metal. Below this threshold, the photon lacks sufficient energy to overcome the binding forces and release an electron.A graph of kinetic energy versus frequency would show a linear relationship with a y-intercept representing the negative work function and a slope equal to Planck’s constant.
The x-intercept represents the threshold frequency.Classical wave theory fails to explain the photoelectric effect because it predicts that the kinetic energy of emitted electrons should depend on the intensity of light, not its frequency, and that electrons should be emitted regardless of the frequency, given sufficient intensity. This is contrary to experimental observations.
Additional Considerations
The simple model described by E photon = Φ + K max has limitations. Factors like electron-electron interactions within the metal can influence the kinetic energy of emitted electrons. These interactions can cause some electrons to lose energy before escaping the surface, resulting in a kinetic energy lower than the maximum predicted by the simple model.The intensity of the incident light affects the number of emitted electrons.
A higher intensity means more photons strike the surface, leading to more electron emissions. However, the maximum kinetic energy of the emitted electrons remains unchanged as long as the frequency remains constant. Each photon still transfers the same amount of energy to the individual electron, regardless of the overall number of photons.
Concise Summary
The photoelectric effect demonstrates that light interacts with matter as particles (photons). When light shines on a metal surface, photons transfer their energy to electrons. If a photon’s energy (hν) exceeds the metal’s work function (Φ), the minimum energy needed to free an electron, the electron is emitted with a maximum kinetic energy (K max) given by E photon = Φ + K max.
The threshold frequency (ν 0 = Φ/h) is the minimum frequency needed for electron emission. The number of emitted electrons depends on light intensity, while their maximum kinetic energy depends only on the light’s frequency.
Experimental Evidence Supporting the Particle Theory
The particle theory of light, suggesting light exists as discrete packets of energy called photons, wasn’t readily accepted. Several crucial experiments provided compelling evidence, solidifying this revolutionary concept and challenging the prevailing wave theory. These experiments demonstrated the quantization of both energy and charge, fundamentally altering our understanding of light and matter interaction.
Millikan’s Oil Drop Experiment
Millikan’s oil drop experiment, conducted in the early 20th century, precisely measured the elementary charge of an electron. This experiment played a pivotal role in supporting the idea of quantized charge, a concept intrinsically linked to the quantized energy observed in the photoelectric effect. The experiment involved suspending tiny oil droplets between two charged plates using an electric field to counter the force of gravity.
Apparatus and Procedure: Millikan’s apparatus consisted of two parallel metal plates, a microscope to observe the oil droplets, an atomizer to create the droplets, and a source of X-rays to ionize the air, charging the oil droplets. By carefully adjusting the voltage between the plates, Millikan could balance the gravitational force pulling the droplet down with the electric force pushing it up.
He observed the motion of the droplets, measuring their terminal velocity both with and without the electric field. A diagram would show two parallel plates with an oil droplet between them, arrows indicating gravitational force downward and electric force upward. The electric field is created by applying a voltage across the plates.
Calculations: By analyzing the terminal velocities, Millikan could calculate the droplet’s charge. He found that the charges on all the droplets were integer multiples of a fundamental unit of charge, e. The equation used involved equating the gravitational force (mg) to the electric force (qE), where m is the mass of the droplet, g is the acceleration due to gravity, q is the charge on the droplet, and E is the electric field strength.
The mass was determined from the droplet’s terminal velocity in the absence of an electric field. The charge (q) was calculated from the voltage required to balance the gravitational force. Millikan repeated this process for many droplets, consistently finding charges that were multiples of a fundamental value, e ≈ 1.602 x 10 -19 Coulombs.
Relevance to the Photoelectric Effect: Millikan’s discovery of the quantized nature of electric charge directly supports the idea of quantized energy in the photoelectric effect. If charge is quantized, it is reasonable to expect that energy, which is intimately related to charge through electromagnetic interactions, would also be quantized. The existence of a fundamental unit of charge implies a fundamental unit of energy, the photon, which is directly involved in the emission of electrons in the photoelectric effect.
Data Analysis and Interpretation: Millikan’s data analysis involved plotting the measured charges of the oil droplets. The data points clustered around integer multiples of a fundamental charge, providing strong evidence for the quantization of charge. Limitations included uncertainties in measuring the droplet’s size and viscosity of the air. However, the consistency of the results across numerous measurements significantly minimized these uncertainties.
The Photoelectric Effect and Quantization of Energy
The photoelectric effect provides direct experimental evidence for the quantization of energy. When light of sufficient frequency shines on a metal surface, electrons are emitted. Crucially, the kinetic energy of these emitted electrons depends solely on the
frequency* of the incident light, not its intensity.
Einstein’s equation for the photoelectric effect, KEmax = hf – Φ , elegantly explains this. Here, KEmax is the maximum kinetic energy of the emitted electrons, h is Planck’s constant, f is the frequency of the incident light, and Φ is the work function of the metal (the minimum energy required to remove an electron from the metal’s surface).
The fact that the kinetic energy of the emitted electrons is linearly dependent on the frequency, and independent of the intensity, directly demonstrates the quantization of light energy. Each photon carries a discrete amount of energy ( hf), and a single photon interacts with a single electron. Increasing the intensity increases the
-number* of photons, but not the energy of each photon, hence not the kinetic energy of the emitted electrons.
Threshold Frequency
The threshold frequency ( f0) is the minimum frequency of light required to eject electrons from a metal surface. Below this frequency, no electrons are emitted, regardless of the light intensity. The threshold frequency is directly related to the work function of the metal by the equation: hf0 = Φ . This relationship further supports the particle nature of light, as only photons with energy greater than or equal to the work function can overcome the binding energy of the electrons and cause emission.
Experimental Setup for Observing the Photoelectric Effect
A typical experimental setup involves a photoemissive metal plate (cathode) and a collecting plate (anode) enclosed in an evacuated tube. Light of a specific frequency shines on the cathode. A variable voltage is applied between the plates. The current (number of emitted electrons) is measured as a function of the applied voltage and light frequency and intensity.
A diagram would show a vacuum tube with a cathode and anode, light source illuminating the cathode, and a voltmeter and ammeter to measure the voltage and current respectively.
Other Experiments Confirming the Particle Nature of Light
Several other experiments independently confirmed the particle nature of light, further strengthening the case against the purely wave theory.
Compton Scattering
Compton scattering involves the inelastic scattering of photons by electrons. When X-rays are scattered by electrons, the scattered X-rays have a longer wavelength (lower frequency) than the incident X-rays. This wavelength shift, known as the Compton shift, cannot be explained by classical wave theory. The Compton shift is given by the equation: Δλ = h/mc (1 – cosθ), where Δλ is the change in wavelength, h is Planck’s constant, m is the electron mass, c is the speed of light, and θ is the scattering angle.
This equation demonstrates that the scattering involves a collision between a photon and an electron, treating the photon as a particle with momentum.
Pair Production
Pair production is the creation of an electron-positron pair from a high-energy photon (gamma ray) near a nucleus. The minimum energy required for pair production is twice the rest mass energy of an electron (2mc² ≈ 1.02 MeV). This process directly demonstrates the energy-mass equivalence (E=mc²) and supports the particle nature of light, as a photon is converted into matter (an electron and a positron).
Conservation laws of energy and momentum are strictly obeyed in this process.
Table of Experiments
| Experiment Name | Key Observation | Conclusion | Relevant Equation(s) |
|---|---|---|---|
| Millikan’s Oil Drop Experiment | Quantized charge on oil droplets | Quantization of electric charge | Felectric = qE; Fgravity = mg |
| Photoelectric Effect | Kinetic energy of emitted electrons depends on frequency, not intensity | Quantization of light energy (photons) | KEmax = hf – Φ |
| Compton Scattering | Wavelength shift of scattered X-rays | Photon momentum and particle-like interaction | Δλ = h/mc (1 – cosθ) |
| Pair Production | Creation of electron-positron pairs from high-energy photons | Energy-mass equivalence; photon as a particle | E = mc² |
Further Exploration
These experiments highlight the wave-particle duality of light, a concept central to quantum mechanics. Classical physics, based on the wave theory of light, failed to explain the photoelectric effect and Compton scattering. The particle nature of light, while seemingly contradictory to its wave-like behavior in phenomena like diffraction and interference, is now a fundamental aspect of our understanding of the universe.
The limitations of classical physics in explaining these phenomena led to the development of quantum mechanics, a theory that successfully incorporates both wave and particle aspects of light and matter.
Wave-Particle Duality of Light
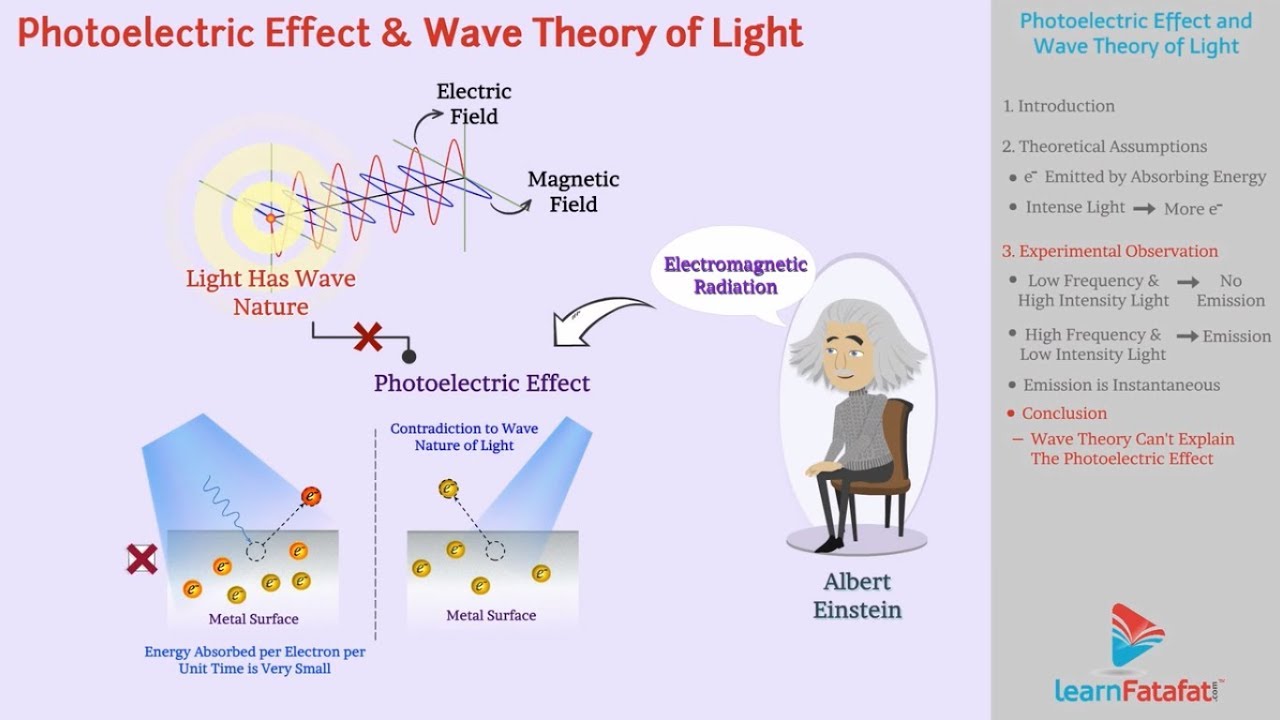
The photoelectric effect, while seemingly straightforward in its demonstration of light’s particle nature, actually highlights a much deeper and more fundamental concept in physics: the wave-particle duality of light. This concept challenges our classical intuition, suggesting that light, and indeed all matter, exhibits properties of both waves and particles depending on how it’s observed. It’s not a case of light
Yo, so the photoelectric effect, right? It’s all about how light kicks electrons outta metal, which totally screams “particle,” not wave. This whole thing kinda blows up Dalton’s idea of atoms being indivisible, check it out: why are some of dalton’s theories not true. See, Dalton didn’t know about subatomic particles, which is why the photoelectric effect’s all, “Nah, bruh, atoms got internal parts that can be ejected by light particles.” It’s a total game-changer, man.
being* either a wave or a particle, but rather displaying aspects of both depending on the experimental context.
The photoelectric effect elegantly demonstrates the particle aspect of light. The observation that electrons are only emitted when light’s frequency exceeds a certain threshold, regardless of intensity, directly contradicts the wave theory of light. A wave’s energy is related to its amplitude (intensity), not its frequency. If light were purely a wave, even a very dim, high-intensity light should eventually eject electrons.
However, this doesn’t happen. The fact that only the frequency matters strongly suggests that light interacts with electrons as discrete packets of energy, or photons, each possessing energy proportional to its frequency.
The Wave and Particle Properties of Light: A Comparison
Light exhibits wave-like properties in phenomena like diffraction and interference. Diffraction, the bending of light around obstacles, and interference, the superposition of waves leading to constructive or destructive patterns, are readily explained by wave models. These phenomena clearly showcase the wave nature of light, such as the characteristic spreading of light waves as they pass through a narrow slit.
The resulting interference pattern, with its alternating bright and dark fringes, is a clear manifestation of wave interference.Conversely, the photoelectric effect, Compton scattering (where light scatters off electrons, changing its wavelength), and the existence of discrete spectral lines in atomic emission and absorption spectra provide compelling evidence for light’s particle-like behavior. In Compton scattering, a photon collides with an electron, transferring some of its energy and momentum, thus changing its wavelength.
This collisional behavior is completely inconsistent with a pure wave description. Similarly, the sharp spectral lines emitted by atoms indicate that electrons in atoms can only exist at specific energy levels, implying a quantized interaction with light – another characteristic of particle behavior. The discrete nature of energy levels suggests a particle-like exchange of energy between light and the atom.
In contrast, a continuous wave model would predict a continuous spectrum of emitted light, not discrete lines.
Applications of the Photoelectric Effect
The photoelectric effect, while a fundamental concept in physics, has far-reaching practical applications across numerous technological fields. Its ability to convert light into electrical energy and its sensitivity to light intensity and frequency have led to the development of a wide range of devices and systems.
Examples of Photoelectric Effect Applications
The photoelectric effect underpins several crucial technologies. Its versatility allows for applications in diverse areas, ranging from medical imaging to industrial automation and consumer electronics.
- Medical Imaging: Photomultiplier tubes (PMTs) are essential components in various medical imaging techniques, such as PET (Positron Emission Tomography) and scintillation counters. They detect and amplify faint light signals emitted by radioactive isotopes or scintillating materials, providing crucial data for diagnosis.
- Industrial Automation: Photoelectric sensors are widely used in industrial automation for tasks like object detection, counting, and level sensing. These sensors utilize the photoelectric effect to detect the presence or absence of objects, enabling precise control in manufacturing processes.
- Consumer Electronics: Photodiodes are found in many consumer electronics, including cameras, remote controls, and light meters. They convert light into electrical signals, enabling functionalities such as image capture, remote control operation, and light level measurement.
- Security Systems: Photoelectric sensors are critical components in security systems, such as burglar alarms and motion detectors. These sensors detect changes in light levels caused by movement, triggering alarms to alert security personnel.
- Spectroscopy: Photoelectric devices are used in various spectroscopic techniques to analyze the composition of materials by measuring the intensity of light absorbed or emitted at different wavelengths. This has applications in environmental monitoring, chemical analysis, and materials science.
Photodiodes and Phototubes
Photodiodes and phototubes are two common devices that leverage the photoelectric effect.
Photodiode
- Materials: Typically made from semiconductor materials like silicon or germanium. A p-n junction is formed within the semiconductor.
- Light Absorption and Electron Emission: When light strikes the semiconductor material, photons with sufficient energy excite electrons in the valence band, allowing them to jump to the conduction band. This generates electron-hole pairs.
- Electrical Signal Generation: The generated electron-hole pairs contribute to an increase in current across the p-n junction. The magnitude of this current is directly proportional to the intensity of the incident light.
- Schematic Diagram:
“`
+—————–+
| |
| p-side | Light
| | —–>
+——–+——–+
| | |
| p-n | n-side |
| junction| |
+——–+——–+
| |
| n-side |
| |
+—————–+
| Current |
+—————–+
“`
Phototube
- Materials: Consists of a photosensitive cathode (usually a metal with a low work function) and an anode enclosed in a vacuum tube.
- Light Absorption and Electron Emission: Incident light on the cathode causes photoemission of electrons.
- Electrical Signal Generation: The emitted electrons are attracted to the positively charged anode, creating a current flow. The magnitude of this current is directly proportional to the light intensity.
- Schematic Diagram:
“`
+—————–+
| |
| Cathode | Light
| | —–>
+—————–+
| |
| Vacuum |
| |
+—————–+
| Anode |
| |
+—————–+
| Current |
+—————–+
“`
Solar Cells and Energy Harvesting
Solar cells directly convert sunlight into electricity using the photovoltaic effect, a manifestation of the photoelectric effect.
- Types of Solar Cells: Silicon-based solar cells are the most common, but thin-film solar cells (using materials like cadmium telluride or copper indium gallium selenide) offer advantages in flexibility and potentially lower cost.
- Photovoltaic Effect: Photons in sunlight strike the semiconductor material of the solar cell, generating electron-hole pairs. These charge carriers are separated by an internal electric field, creating a current that can power external circuits.
- Limitations and Challenges: Solar cell efficiency is limited by factors like material properties, temperature, and light intensity. Material costs, manufacturing processes, and the environmental impact of manufacturing and disposal are also important considerations.
- Comparison with Other Technologies: While other energy-harvesting technologies exist (e.g., thermoelectric generators), solar cells represent the most widespread and practical application of the photoelectric effect for large-scale energy generation.
Comparison of Light-Matter Interactions
| Feature | Photoelectric Effect | Compton Scattering | Photoionization |
|---|---|---|---|
| Interaction Type | Photon absorption by an electron | Inelastic scattering of a photon by an electron | Photon absorption by an atom, leading to electron ejection |
| Energy Transfer | Complete photon energy transferred to electron | Partial photon energy transferred to electron | Photon energy sufficient to overcome ionization energy |
| Resulting Effect | Electron emission | Photon wavelength shift, electron recoil | Ion formation, electron emission |
Detailed Application: PET Scanners
Positron Emission Tomography (PET) scanners utilize the photoelectric effect within photomultiplier tubes (PMTs). Radioactive tracers emit positrons, which annihilate with electrons, producing two gamma rays. These gamma rays strike a scintillator crystal, causing it to emit photons. These photons are then detected by PMTs. The PMTs amplify the weak light signals, allowing for the precise localization of the tracer within the body, creating detailed images of metabolic activity.
The number of photons detected is proportional to the concentration of the tracer, providing crucial diagnostic information.
Historical Context
Early experiments on the photoelectric effect, particularly those by Heinrich Hertz and Philipp Lenard, revealed its puzzling behavior—the independence of electron emission from light intensity and its dependence on frequency. This couldn’t be explained by classical wave theory.
“Einstein’s explanation of the photoelectric effect, which postulated the existence of light quanta (photons), revolutionized our understanding of light and matter interaction.”
Future Advancements
Future advancements in the application of the photoelectric effect are likely to focus on improving solar cell efficiency through new materials and designs, developing more sensitive and efficient photodetectors for advanced imaging and sensing applications, and exploring novel applications in areas like quantum information processing. The ongoing research into perovskite solar cells, for example, shows significant promise in increasing efficiency and reducing costs.
Limitations of the Classical Wave Theory

The classical wave theory, while successfully explaining many aspects of light’s behavior, failed to account for the key observations of the photoelectric effect. This failure highlighted fundamental limitations in the understanding of light-matter interactions and paved the way for the development of quantum mechanics. The following sections detail these limitations.
Key Limitations of the Classical Wave Theory in Explaining the Photoelectric Effect
Classical wave theory, which treats light as a continuous wave, predicted behaviors inconsistent with experimental observations of the photoelectric effect. Three major limitations are Artikeld below.
- Intensity Dependence of Electron Emission: Classical theory predicted that increasing light intensity would increase the kinetic energy of emitted electrons. This is because a more intense wave would transfer more energy to the electrons. However, experiments showed that intensity only affects the
-number* of emitted electrons, not their kinetic energy. - Frequency Dependence of Electron Emission: Classical theory did not predict a threshold frequency below which no electrons would be emitted, regardless of intensity. It suggested that even low-frequency light, given sufficient intensity, could eventually impart enough energy to release electrons. Experiments, however, demonstrated a clear frequency threshold.
- Instantaneous Electron Emission: Classical wave theory predicted a time delay between light exposure and electron emission, as the electron would need time to absorb sufficient energy from the wave. Experiments showed instantaneous emission, contradicting this prediction.
| Observation | Classical Wave Theory Prediction | Discrepancy |
|---|---|---|
| Increasing light intensity increases the number of emitted electrons, but not their kinetic energy. | Increasing light intensity increases the kinetic energy of emitted electrons. | Classical theory fails to predict the independence of kinetic energy from intensity. |
| There is a threshold frequency below which no electrons are emitted, regardless of intensity. | Electrons should be emitted at any frequency, given sufficient intensity. | Classical theory fails to predict the existence of a threshold frequency. |
| Electron emission is instantaneous. | There should be a time delay between light exposure and electron emission. | Classical theory fails to predict the instantaneous nature of electron emission. |
Failure of the Wave Theory to Account for Instantaneous Electron Emission
Classical wave theory suggests that electrons absorb energy gradually from the incident light wave. The time required for an electron to absorb enough energy to overcome the work function (the minimum energy needed to escape the material) would lead to a measurable time delay before emission. However, experimental observations consistently show instantaneous electron emission upon light exposure, regardless of the light intensity.
This discrepancy directly challenges the continuous energy absorption model of the classical wave theory. The intensity of the light wave, according to classical physics, would only influence therate* at which energy is absorbed, not the time it takes to reach the threshold for emission. This contradicts the experimental observation of instantaneous emission, irrespective of intensity. A mathematical description would involve calculating the time required for energy absorption based on the intensity and frequency of the wave, which would invariably predict a non-zero delay, unlike the experimental observation.
Comparison of Wave and Particle Theory Predictions Regarding Light Intensity
- Classical Wave Theory: Predicts that increasing light intensity increases the kinetic energy of emitted electrons. A higher intensity wave transfers more energy per unit time to the electrons.
- Particle Theory (Quantum Theory): Predicts that increasing light intensity increases the
-number* of emitted electrons, but the kinetic energy of individual electrons remains constant (for a given frequency). Higher intensity means more photons, each with sufficient energy to release an electron, leading to more electrons being emitted.
A graph would show a linear, positive relationship between kinetic energy and intensity for the classical wave theory and a horizontal line representing constant kinetic energy regardless of intensity for the particle theory.
Role of Frequency in the Photoelectric Effect According to Classical and Particle Theories
- Classical Wave Theory: Predicts that light frequency plays a minor role; the energy transferred depends primarily on intensity. A higher intensity wave, regardless of frequency, would eventually deliver enough energy to liberate electrons.
- Particle Theory (Quantum Theory): Predicts that the frequency of light directly determines the kinetic energy of emitted electrons. Each photon carries energy proportional to its frequency (E = hf, where h is Planck’s constant and f is frequency). A minimum frequency (threshold frequency) is required to provide enough energy to overcome the work function. Higher frequencies lead to higher kinetic energies of emitted electrons.
The experimental observation of a threshold frequency and the linear relationship between frequency and maximum kinetic energy strongly support the particle theory and refute the classical wave theory’s prediction. This is extensively documented in numerous physics textbooks and research papers. For example, Millikan’s experiments in the early 20th century provided crucial experimental evidence supporting Einstein’s photoelectric effect explanation (Millikan, R.
A. (1916). A direct photoelectric determination of Planck’s h.
- Physical Review*,
- 7*(3), 355.).
Implications of the Failure of the Classical Wave Theory for the Development of Quantum Mechanics
The failure of the classical wave theory to explain the photoelectric effect was a pivotal moment in the development of quantum mechanics. This failure demonstrated the limitations of classical physics in describing phenomena at the atomic and subatomic levels.
- Quantization of Energy: The success of Einstein’s explanation, which introduced the concept of light quanta (photons), demonstrated that energy is not continuous but exists in discrete packets. This concept of quantization is fundamental to quantum mechanics.
- Einstein’s Contribution: Einstein’s 1905 paper on the photoelectric effect provided the first compelling evidence for the particle nature of light and was a cornerstone of the quantum revolution. It demonstrated that light, despite exhibiting wave-like properties, also behaves as a stream of particles.
The key conceptual shifts resulting from this failure included the acceptance of:
- The particle nature of light
- The quantization of energy
- The inadequacy of classical physics at the atomic scale
Planck’s Quantum Hypothesis and its Significance
Before Einstein’s explanation of the photoelectric effect, Max Planck’s groundbreaking work laid the crucial foundation. His quantum hypothesis revolutionized our understanding of energy and paved the way for the acceptance of light’s particle-like nature. It provided the theoretical framework necessary to fully comprehend the experimental observations of the photoelectric effect that defied classical physics.Planck’s quantum hypothesis proposed that energy is not emitted or absorbed continuously, as classical physics suggested, but rather in discrete packets called quanta.
These quanta are directly proportional to the frequency of the radiation. This seemingly simple idea had profound implications, completely reshaping our understanding of the interaction between light and matter. It directly addressed the inability of the wave theory to explain the photoelectric effect, where the energy of emitted electrons depended solely on the frequency of light, not its intensity.
Planck’s Constant and Photon Energy
The energy of a single quantum, or photon, is directly proportional to its frequency. This relationship is expressed by the famous equation:
E = hf
where ‘E’ represents the energy of the photon, ‘f’ represents its frequency, and ‘h’ is Planck’s constant, a fundamental constant in physics with a value of approximately 6.626 x 10 -34 joule-seconds. This equation shows that higher frequency light (like ultraviolet light) carries photons with more energy than lower frequency light (like red light). This energy difference directly explains why only light above a certain threshold frequency can eject electrons in the photoelectric effect, regardless of intensity.
For instance, low-intensity ultraviolet light can still eject electrons because each photon carries enough energy, whereas high-intensity red light fails because individual photons lack sufficient energy.
Impact on Quantum Mechanics
Planck’s quantum hypothesis marked the birth of quantum mechanics. His work challenged the established classical view of physics, opening the door to a new era of understanding the behavior of matter at the atomic and subatomic levels. The concept of quantized energy, initially applied to the emission of light from heated objects (blackbody radiation), proved essential in explaining numerous other phenomena, including the photoelectric effect, the spectrum of atomic emissions, and the stability of atoms.
It formed the bedrock upon which Einstein, Bohr, Heisenberg, Schrödinger, and many others built the sophisticated framework of quantum mechanics, which governs the world at the smallest scales and underpins many modern technologies. Without Planck’s revolutionary idea, our understanding of the universe at a fundamental level would be vastly different.
The Concept of Photons
The photoelectric effect’s explanation hinges on the revolutionary concept of the photon, a fundamental particle of light. Understanding photons is crucial to grasping why classical wave theory failed to account for experimental observations. This section will delve into the properties of photons and how they interact with matter in the context of the photoelectric effect.Photons are discrete packets of electromagnetic energy, each carrying a specific amount of energy.
This energy is directly proportional to the frequency of the light, a relationship described by Einstein’s famous equation,
E = hf
, where ‘E’ represents the energy of the photon, ‘h’ is Planck’s constant (approximately 6.626 x 10 -34 Js), and ‘f’ is the frequency of the light. Unlike classical waves, which can have any amount of energy, photons exist as individual, indivisible units.
Photon-Matter Interaction in the Photoelectric Effect
In the photoelectric effect, a photon interacts with a single electron in a metal. If the photon’s energy (hf) is greater than the work function (Φ) of the metal – the minimum energy required to remove an electron from the metal’s surface – the electron absorbs the entire photon’s energy. This energy transfer is an instantaneous process; the electron is either ejected or it isn’t.
There’s no gradual energy accumulation as predicted by the classical wave theory. The excess energy (hf – Φ) is converted into the kinetic energy of the emitted electron. If the photon’s energy is less than the work function, no electrons are emitted, regardless of the intensity of the light.
Comparison of Photons and Classical Waves
Classical wave theory describes light as a continuous wave with its energy distributed across the wavefront. The intensity of the light, according to this theory, is directly related to the amplitude of the wave, and therefore, the energy it carries. This implies that increasing the intensity of light should increase the kinetic energy of the emitted electrons and the number of emitted electrons.
However, experimental observations contradict this. Increasing intensity only increases the number of emitted electrons, not their kinetic energy. This is a key difference between the particle and wave descriptions of light. Photons, on the other hand, are discrete packets of energy, and their energy is directly proportional to their frequency, not their intensity. The intensity of light corresponds to the number of photons, not the energy of individual photons.
This explains why increasing the intensity of low-frequency light doesn’t cause electron emission, while even a weak beam of high-frequency light can eject electrons.
Creating a Table Summarizing Key Differences
The following table directly compares the predictions of classical wave theory with the experimental observations of the photoelectric effect. This comparison highlights the fundamental discrepancies that ultimately led to the acceptance of the quantum theory of light.
A key aspect of understanding the photoelectric effect lies in contrasting the predictions of classical wave theory with experimental results. Classical physics, based on the understanding of light as a continuous wave, failed to explain several crucial observations. The discrepancies revealed the need for a radical new approach to understanding light and matter interaction, ultimately leading to the development of quantum mechanics.
Comparison of Classical Wave Theory and Experimental Observations of the Photoelectric Effect
| Prediction (Classical Wave Theory) | Experimental Observation | Discrepancy | Resolution (Quantum Explanation) |
|---|---|---|---|
| Increasing light intensity increases electron kinetic energy. | Increasing light intensity increases electron current, but not kinetic energy. | Kinetic energy is independent of intensity. | Light energy is quantized into photons; intensity affects the number of photons, not their energy. |
| Electron kinetic energy is independent of light frequency. | Electron kinetic energy is directly proportional to light frequency (Ek = hf – φ). | Kinetic energy depends on frequency. | Each photon carries energy proportional to its frequency (E = hf); only photons with sufficient energy (above the work function φ) can eject electrons. |
| There should be no threshold frequency for electron emission. | There exists a threshold frequency (f0) below which no electrons are emitted, regardless of intensity. | Existence of a threshold frequency. | Electrons only get ejected if a single photon’s energy (hf) is greater than or equal to the work function (φ) of the metal (hf ≥ φ). |
| There should be a time delay between light incidence and electron emission, dependent on intensity. | Electron emission is essentially instantaneous, even at low intensities. | Instantaneous emission, independent of intensity. | A single photon interaction is sufficient to eject an electron; no time is needed to accumulate energy from a wave. |
| Electron current should increase gradually with increasing intensity. | Electron current is directly proportional to light intensity above the threshold frequency. | Linear relationship between current and intensity above threshold. | Higher intensity means more photons, hence more electrons emitted. |
Discrepancy Explanations: The classical wave theory predicted a gradual increase in electron kinetic energy with increasing light intensity, failing to account for the observed independence of kinetic energy from intensity. It also failed to predict the existence of a threshold frequency, the instantaneous emission of electrons, and the linear relationship between current and intensity above the threshold. The quantum explanation, proposing that light exists as discrete packets of energy called photons, successfully resolves all these discrepancies.
Each photon carries a specific energy (E=hf), and a single photon interaction is sufficient to eject an electron, provided its energy exceeds the material’s work function.
The photoelectric effect stands as a pivotal experiment in the development of quantum mechanics. The experimental observations directly contradicted the predictions of classical wave theory, demonstrating the inadequacy of classical physics in explaining the interaction of light and matter at the atomic level. The successful explanation by Einstein, using Planck’s quantum hypothesis, provided compelling evidence for the particle nature of light and paved the way for a new understanding of the quantum world, fundamentally altering our perception of light and matter.
Illustrating the Photoelectric Effect
The photoelectric effect is best understood through a visual representation of the interaction between light and a metal surface. The following description details a diagram illustrating this fundamental quantum phenomenon.A simple illustration would show a beam of light, represented by a series of arrows or wavy lines, directed towards a metal surface. The metal surface is depicted as a solid block with a regular arrangement of atoms, visually representing the crystalline structure.
Each atom in the metal possesses electrons, shown as smaller circles orbiting the atomic nuclei. Crucially, some of these electrons are loosely bound to the metal and can be easily removed.
Photon-Metal Interaction
The illustration should clearly show one photon from the light beam striking a specific electron within the metal. The photon is represented as a discrete packet of energy, often depicted as a small bundle or a particle with a wavy line representing its wave-like nature. This collision between the photon and the electron is the central event in the photoelectric effect.
The energy transferred from the photon to the electron is depicted as an arrow indicating the direction and magnitude of the energy transfer. This transfer is only successful if the photon possesses sufficient energy (determined by its frequency).
Electron Ejection
If the photon’s energy exceeds the work function of the metal (the minimum energy required to remove an electron), the electron absorbs this energy and is ejected from the metal surface. The ejected electron is shown as a smaller circle moving away from the metal surface with a velocity vector indicating its kinetic energy. This kinetic energy is directly related to the difference between the photon’s energy and the metal’s work function.
The illustration should clearly distinguish between the initial state (electron bound to the atom) and the final state (electron ejected with kinetic energy).
Labels in the Illustration
The illustration should include clear labels: “Incident Light,” “Metal Surface,” “Photon,” “Electron,” “Work Function (Φ),” “Kinetic Energy (KE),” and “Ejected Electron.” The direction of the light beam, the energy transfer from the photon to the electron, and the direction of the ejected electron should all be clearly indicated using arrows. The energy levels of the electron, both before and after the interaction, could be visually represented using energy level diagrams, showing the energy difference between the bound and free states.
This complete depiction visually summarizes the key aspects of the photoelectric effect.
Threshold Frequency and Work Function
The threshold frequency and work function are crucial parameters in understanding the photoelectric effect. They represent the minimum energy requirements for electron emission from a metal surface when exposed to light. The work function is the minimum energy needed to remove an electron from the surface, while the threshold frequency is the minimum frequency of light that possesses this energy.
Their relationship is fundamental to the particle nature of light.
- Metal: Sodium
- Threshold Frequency (ν₀): 5.5 × 10 14 Hz
- Work Function (Φ): 2.3 eV
- Source: Serway, R. A., & Jewett, J. W. (2018). Physics for scientists and engineers with modern physics (10th ed.).
Cengage Learning.
- Metal: Potassium
- Threshold Frequency (ν₀): 5.0 × 10 14 Hz
- Work Function (Φ): 2.2 eV
- Source: Serway, R. A., & Jewett, J. W. (2018). Physics for scientists and engineers with modern physics (10th ed.).
Cengage Learning.
- Metal: Cesium
- Threshold Frequency (ν₀): 4.5 × 10 14 Hz
- Work Function (Φ): 2.1 eV
- Source: Serway, R. A., & Jewett, J. W. (2018). Physics for scientists and engineers with modern physics (10th ed.).
Cengage Learning.
- Metal: Zinc
- Threshold Frequency (ν₀): 1.0 × 10 15 Hz
- Work Function (Φ): 4.3 eV
- Source: Serway, R. A., & Jewett, J. W. (2018). Physics for scientists and engineers with modern physics (10th ed.).
Cengage Learning.
- Metal: Platinum
- Threshold Frequency (ν₀): 1.3 × 10 15 Hz
- Work Function (Φ): 6.35 eV
- Source: Serway, R. A., & Jewett, J. W. (2018). Physics for scientists and engineers with modern physics (10th ed.).
Cengage Learning.
Comparison of Threshold Frequency and Work Function for Different Metals
| Metal | Threshold Frequency (Hz) | Work Function (eV) | Source |
|---|---|---|---|
| Cesium | 4.5 × 1014 | 2.1 | Serway & Jewett (2018) |
| Potassium | 5.0 × 1014 | 2.2 | Serway & Jewett (2018) |
| Sodium | 5.5 × 1014 | 2.3 | Serway & Jewett (2018) |
| Zinc | 1.0 × 1015 | 4.3 | Serway & Jewett (2018) |
| Platinum | 1.3 × 1015 | 6.35 | Serway & Jewett (2018) |
Relationship Between Threshold Frequency and Work Function
The threshold frequency and work function are directly proportional. A higher work function, meaning more energy is required to remove an electron, corresponds to a higher threshold frequency. This is because the energy of a photon is directly proportional to its frequency (E = hν), so a higher frequency is needed to provide the necessary energy to overcome the work function.
Mathematical Relationship Between Threshold Frequency, Work Function, and Planck’s Constant
The relationship is described by the equation: Φ = hν₀
where:* Φ is the work function
- h is Planck’s constant
- ν₀ is the threshold frequency
Graphical Representation of the Relationship
The graph would show a linear relationship between work function (y-axis) and threshold frequency (x-axis). The data points for each metal (Cesium, Potassium, Sodium, Zinc, Platinum) would lie on a straight line passing through the origin. The slope of this line would represent Planck’s constant. (Note: A graphical representation cannot be created in this text-based format.)
Calculation of Planck’s Constant
Using the equation Φ = hν₀, we can calculate Planck’s constant (h) for three metals:* Cesium: h = Φ/ν₀ = (2.1 eV1.602 × 10 -19 J/eV) / (4.5 × 10 14 Hz) ≈ 7.5 × 10 -34 Js
Potassium
h = Φ/ν₀ = (2.2 eV
- 1.602 × 10 -19 J/eV) / (5.0 × 10 14 Hz) ≈ 7.1 × 10 -34 Js
- 1.602 × 10 -19 J/eV) / (1.0 × 10 15 Hz) ≈ 6.9 × 10 -34 Js
Zinc
h = Φ/ν₀ = (4.3 eV
The calculated values of h are reasonably consistent, considering the approximations involved. Discrepancies may arise from inaccuracies in the experimental determination of the threshold frequency and work function.
Limitations in Determining Planck’s Constant
The accuracy of Planck’s constant calculated using this method is limited by the precision of the experimental measurements of the threshold frequency and work function. Factors such as surface contamination, temperature variations, and the inherent limitations of the measurement techniques can introduce errors. Furthermore, the values used here are likely rounded and represent average values rather than exact measurements for a specific sample.
Using more precise data from controlled experiments would yield a more accurate result.
Energy Conservation in the Photoelectric Effect
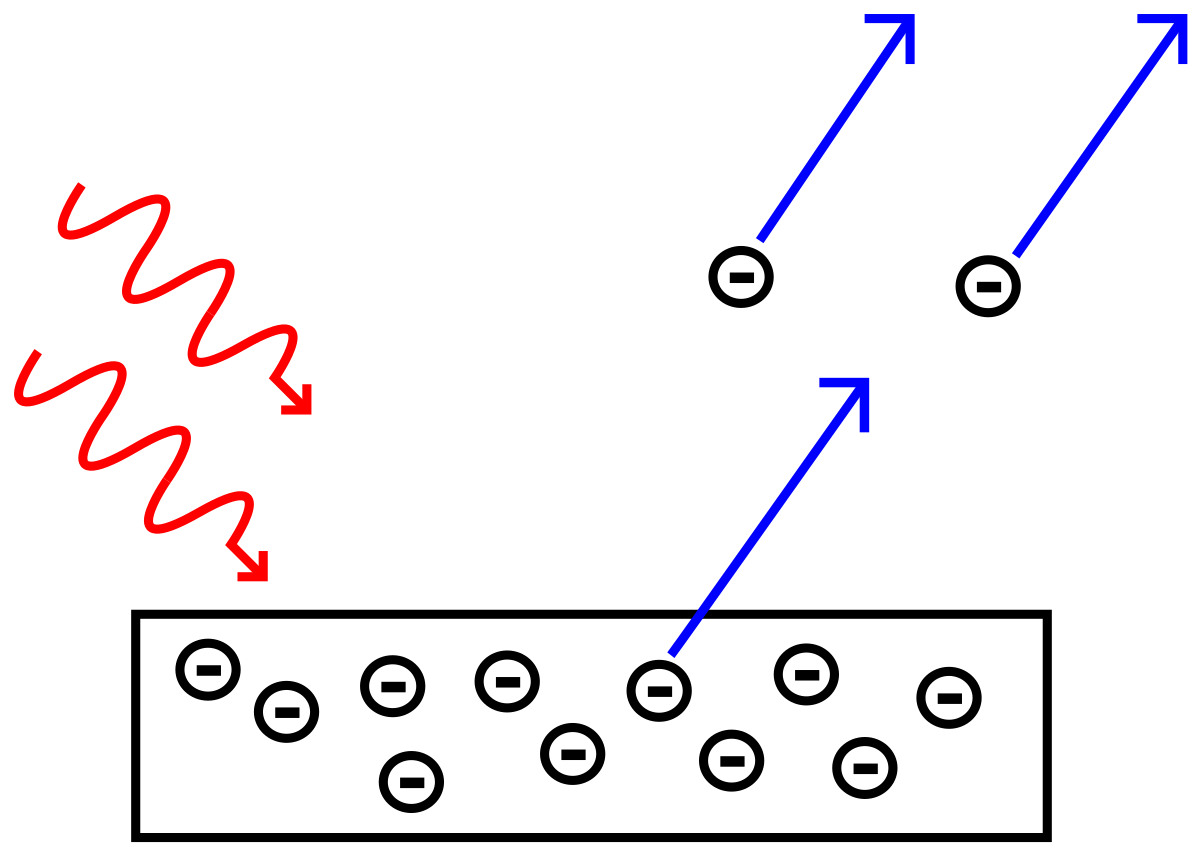
The photoelectric effect elegantly demonstrates the principle of energy conservation. Incoming light energy is transformed into kinetic energy of emitted electrons and the energy required to overcome the material’s binding energy. This conversion process is precisely described by Einstein’s equation, providing a powerful validation of both energy conservation and the particle nature of light.The total energy of the incoming photon is entirely accounted for in the outcome of the photoelectric process.
No energy is mysteriously lost or gained; it’s simply transferred and transformed. This conservation principle is crucial for understanding the effect and for validating Einstein’s explanation over the shortcomings of classical wave theory.
Einstein’s Photoelectric Equation and Energy Conservation
Einstein’s famous equation for the photoelectric effect mathematically expresses energy conservation:
Ephoton = KE max + Φ
Where:* Ephoton represents the energy of the incident photon, which is directly proportional to its frequency ( Ephoton = hf , where h is Planck’s constant and f is the frequency).
- KEmax is the maximum kinetic energy of the emitted electron. This represents the energy the electron possesses after overcoming the material’s binding energy.
- Φ (Phi) is the work function of the material. This is the minimum energy required to remove an electron from the surface of the material. It’s essentially the binding energy of the electron to the material.
This equation shows that the energy of the incoming photon is completely used up in two ways: a portion is used to overcome the work function (freeing the electron), and the remaining portion is converted into the kinetic energy of the ejected electron. If the photon’s energy ( hf) is less than the work function ( Φ), no electrons will be emitted, regardless of the light intensity.
Illustrative Example of Energy Conservation
Let’s consider a specific example. Suppose we shine light with a frequency of 1.0 x 10 15 Hz onto a metal surface with a work function of 4.0 eV. Planck’s constant (h) is approximately 4.136 x 10 -15 eV·s.First, we calculate the photon energy:
Ephoton = hf = (4.136 x 10 -15 eV·s)(1.0 x 10 15 Hz) = 4.136 eV
Since the photon energy (4.136 eV) is greater than the work function (4.0 eV), electrons will be emitted. The maximum kinetic energy of the emitted electrons can be calculated:
KEmax = E photon
Φ = 4.136 eV – 4.0 eV = 0.136 eV
This demonstrates that the energy of the incident photon is precisely conserved; it’s completely used to overcome the work function and provide kinetic energy to the emitted electron. This clear energy balance is a hallmark of the photoelectric effect and a strong piece of evidence supporting the particle theory of light.
Further Exploration of Quantum Phenomena
The photoelectric effect wasn’t just a fascinating anomaly; it served as a pivotal experiment, shattering the classical understanding of light and paving the way for the development of quantum mechanics. Its inexplicable results, defying classical wave theory, forced physicists to rethink fundamental concepts about energy, matter, and the interaction between them. This led to a cascade of new theories and discoveries, fundamentally altering our understanding of the universe at its most basic level.The successful explanation of the photoelectric effect using Einstein’s concept of light quanta (photons) directly contradicted the wave theory of light, which had been dominant for centuries.
This provided the crucial first step towards accepting the dual nature of light – exhibiting both wave-like and particle-like properties. This dual nature, a cornerstone of quantum mechanics, became a central theme in subsequent research, influencing countless advancements in physics and related fields.
The Development of Quantum Mechanics
Einstein’s explanation of the photoelectric effect, while groundbreaking, was just the beginning. It spurred further investigations into the quantized nature of energy and matter. The subsequent development of quantum mechanics, a revolutionary theory describing the behavior of matter and energy at the atomic and subatomic levels, owes a significant debt to the insights gained from the photoelectric effect.
This new theory successfully explained phenomena that classical physics couldn’t, including atomic spectra, the stability of atoms, and the behavior of electrons in materials. Many key concepts of quantum mechanics, such as wave-particle duality and the uncertainty principle, were either directly inspired by or refined through the lens of the photoelectric effect. For instance, the concept of quantization of energy, a core principle of quantum mechanics, was directly demonstrated by the effect’s dependence on light frequency.
Influence on Other Scientific Fields
The implications of the photoelectric effect extended far beyond theoretical physics. Its practical applications have revolutionized numerous technologies. The understanding of how light interacts with matter at the atomic level, as revealed by the photoelectric effect, led to the development of photoelectric devices such as photodiodes, phototransistors, and photomultiplier tubes. These devices are crucial components in various technologies, including solar cells, digital cameras, and medical imaging equipment.
The impact of the photoelectric effect can be seen in everyday life, from the electricity generated by solar panels to the images captured by our smartphones. Furthermore, the theoretical underpinnings of the photoelectric effect have influenced fields such as chemistry, materials science, and nanotechnology, leading to innovations in areas like photocatalysis and the development of new materials with tailored optical properties.
Answers to Common Questions
What are some limitations of Einstein’s photoelectric effect model?
Einstein’s model simplifies the interaction, neglecting factors like electron-electron interactions within the metal and surface irregularities. It also assumes instantaneous electron emission, which isn’t entirely accurate at very low light intensities.
How does the photoelectric effect relate to wave-particle duality?
The effect showcases wave-particle duality: light behaves as a wave in its propagation but as a particle (photon) in its interaction with matter, transferring energy in discrete packets.
What are some real-world applications beyond solar cells?
Photoelectric devices are crucial in photodiodes (light sensors), photomultiplier tubes (used in medical imaging), and various industrial sensors and control systems.
Why was the photoelectric effect so significant historically?
It directly challenged classical physics, demonstrating the limitations of classical wave theory and paving the way for the development of quantum mechanics, a profound shift in scientific understanding.