Why are some of Dalton’s theories not true? This compelling question unveils a fascinating journey through the evolution of atomic theory. John Dalton’s groundbreaking work revolutionized chemistry, providing the first comprehensive atomic model. Yet, like all scientific advancements, his postulates were later refined and even revised in light of new discoveries. Exploring these limitations not only illuminates the scientific method’s iterative nature but also highlights the enduring power of scientific inquiry and our ever-evolving understanding of the universe.
Dalton’s model, though revolutionary for its time, rested on assumptions that subsequent research proved incomplete. His concept of indivisible atoms, for instance, was challenged by the discovery of subatomic particles. Similarly, the idea of identical atoms of a single element was refined with the understanding of isotopes. This exploration delves into the specific inaccuracies, examining the experimental evidence that led to these revisions and celebrating the enduring legacy of Dalton’s contributions to the field of chemistry.
Dalton’s Atomic Theory

Dalton’s atomic theory, developed in the early 1800s, revolutionized our understanding of matter. While not entirely accurate by today’s standards, it laid the groundwork for modern chemistry and provided a crucial framework for interpreting chemical reactions. This exploration delves into the postulates of Dalton’s theory, their implications, limitations, and their comparison with modern atomic theory.
Dalton’s Atomic Theory: The Postulates
The following bullet points summarize Dalton’s five postulates. These simple yet groundbreaking ideas fundamentally changed how scientists viewed the composition of matter.
- All matter is made of atoms, which are indivisible and indestructible.
- All atoms of a given element are identical in mass and properties.
- Atoms of different elements have different masses and properties.
- Atoms combine in simple, whole-number ratios to form chemical compounds.
- In chemical reactions, atoms are combined, separated, or rearranged, but never created or destroyed.
Detailed Explanation of Dalton’s Postulates
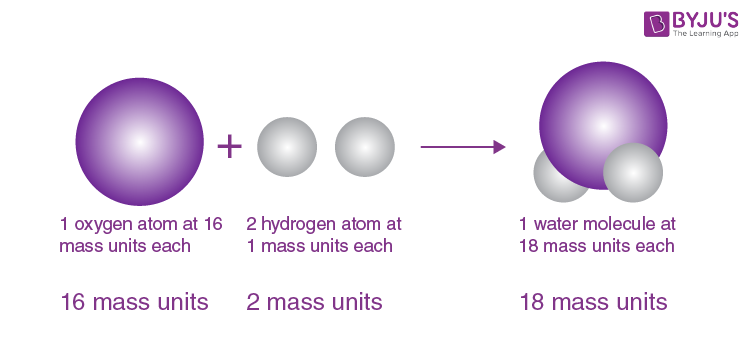
- All matter is made of atoms, which are indivisible and indestructible. This postulate implies that matter is composed of tiny, fundamental particles. It suggests that chemical reactions involve the rearrangement of these atoms, not their creation or destruction. For example, in the reaction between hydrogen and oxygen to form water (2H₂ + O₂ → 2H₂O), the hydrogen and oxygen atoms are rearranged to form water molecules; no atoms are lost or gained.
- All atoms of a given element are identical in mass and properties. This postulate suggests that all atoms of a specific element, such as carbon, are exactly alike in terms of mass and chemical behavior. This simplifies our understanding of elements. For instance, all carbon atoms have the same atomic number and almost the same mass. This allows for consistent predictions in chemical reactions involving carbon.
- Atoms of different elements have different masses and properties. This postulate distinguishes between different types of atoms. For example, hydrogen atoms are much lighter and have different chemical properties than oxygen atoms. This difference in properties is reflected in the vastly different chemical behaviors of hydrogen and oxygen.
- Atoms combine in simple, whole-number ratios to form chemical compounds. This is the basis of Dalton’s Law of Multiple Proportions. The formation of compounds occurs when atoms of different elements combine in simple whole-number ratios. For instance, water (H₂O) always forms with a 2:1 ratio of hydrogen to oxygen atoms. This ratio is always consistent, regardless of the amount of water produced.
- In chemical reactions, atoms are combined, separated, or rearranged, but never created or destroyed. This postulate reflects the law of conservation of mass. In any chemical reaction, the total mass of the reactants equals the total mass of the products. This is evident in combustion reactions, where the mass of the reactants (fuel and oxygen) equals the mass of the products (carbon dioxide, water, and ash).
Comparison of Dalton’s and Modern Atomic Theory
The following table compares and contrasts Dalton’s postulates with modern atomic theory.
| Dalton’s Postulate | Modern Atomic Theory | Comparison/Contrast |
|---|---|---|
| All matter is composed of indivisible atoms. | Atoms are composed of subatomic particles (protons, neutrons, electrons). | Dalton’s postulate is incorrect; atoms are divisible. |
| All atoms of a given element are identical in mass and properties. | Atoms of the same element can have different masses (isotopes). | Dalton’s postulate is partially incorrect; isotopes exist. |
| Atoms of different elements have different masses and properties. | Atoms of different elements have different numbers of protons and different properties. | This postulate is largely correct. |
| Atoms combine in simple, whole-number ratios to form chemical compounds. | Atoms combine in whole-number ratios to form compounds; however, the ratios can be more complex than Dalton envisioned. | This postulate is largely correct, but modern theory accounts for more complex compounds. |
| In chemical reactions, atoms are combined, separated, or rearranged, but never created or destroyed. | In chemical reactions, atoms are rearranged; the total number of atoms remains constant (law of conservation of mass). | This postulate remains largely correct. |
Dalton’s Law of Multiple Proportions
Dalton’s Law of Multiple Proportions states that when two elements form more than one compound, the ratios of the masses of the second element that combine with a fixed mass of the first element will be ratios of small whole numbers.
- Carbon Monoxide (CO) and Carbon Dioxide (CO₂): In CO, the ratio of carbon to oxygen is 12:16 (approximately 3:4). In CO₂, the ratio is 12:32 (approximately 3:8). The ratio of oxygen in CO₂ to oxygen in CO is 32:16, or 2:1, a simple whole-number ratio. This supports Dalton’s postulate about simple whole-number ratios in compound formation.
- Nitrogen Oxide (NO) and Nitrogen Dioxide (NO₂): In NO, the ratio of nitrogen to oxygen is approximately 14:16 (7:8). In NO₂, the ratio is approximately 14:32 (7:16). The ratio of oxygen in NO₂ to oxygen in NO is 32:16, or 2:1, again a simple whole-number ratio, supporting Dalton’s postulate.
Limitations of Dalton’s Atomic Theory
Dalton’s model, while revolutionary, had limitations. His theory couldn’t explain certain phenomena discovered later.
The key limitations of Dalton’s atomic theory include the divisibility of atoms (the existence of subatomic particles), the existence of isotopes (atoms of the same element with different masses), and the fact that atoms of the same element can have slightly different masses. These limitations were overcome by subsequent discoveries in nuclear physics and advancements in mass spectrometry.
Limitations of Dalton’s Model

Yo, Jogja peeps! So, we’ve talked about Dalton’s atomic theory – a pretty groundbreaking idea for its time. But like, even the coolest theories have their flaws, right? Let’s dive into where Dalton’s model fell a bit short.
Subatomic Particles and the Challenge to Dalton’s Model
Dalton thought atoms were solid, indivisible spheres – like tiny, indestructible billiard balls. But then,
- boom*! Scientists started discovering stuff
- inside* those atoms. Experiments, like J.J. Thomson’s cathode ray tube experiments, revealed the electron – a negatively charged particle way smaller than even Dalton’s smallest atom. Later, Rutherford’s gold foil experiment showed that atoms have a tiny, dense, positively charged nucleus, leading to the discovery of protons. And finally, Chadwick discovered the neutron, a neutral particle also residing in the nucleus.
These discoveries totally smashed Dalton’s idea of the atom as a fundamental, indivisible unit. It was like finding out your favorite game console is actually made of even smaller, more awesome components!
Isotopes and the Indivisibility of Atoms
Dalton also believed all atoms of a particular element were identical. But,plot twist*, isotopes exist! Isotopes are atoms of the same element with the same number of protons but a different number of neutrons. This means they have the same atomic number but different mass numbers. For example, carbon-12 and carbon-14 are both carbon, but they have different numbers of neutrons, meaning they have different masses.
This directly contradicts Dalton’s idea that all atoms of an element are identical and indivisible. It’s like discovering your favorite band has secretly released two slightly different versions of the same album!
Comparison of Dalton’s and Modern Atomic Models
Okay, let’s break it down with a table to see the differences clearly. This is where things get
real* interesting.
| Feature | Dalton’s Model (Early 1800s) | Modern Atomic Model |
|---|---|---|
| Atom’s Nature | Solid, indivisible sphere | Complex structure with subatomic particles (protons, neutrons, electrons) |
| Atomic Mass | All atoms of an element have the same mass | Atoms of the same element can have different masses (isotopes) |
| Subatomic Particles | None proposed | Protons, neutrons, and electrons |
| Atomic Structure | No internal structure described | Nucleus (containing protons and neutrons) surrounded by electrons |
Isotopes and Atomic Mass: Why Are Some Of Dalton’s Theories Not True

Yo, Jogja peeps! So, we’ve been chatting about Dalton’s atomic theory, which was pretty groundbreaking for its time. But like, even the coolest theories have their flaws, right? One major crack in Dalton’s awesome model is its inability to fully explain isotopes and their varying atomic masses. Let’s dive into that!Dalton thought all atoms of the same element were identical, like twins.
But that’s not entirely true. Isotopes are where things get interesting.
Isotope Examples and Challenges to Dalton’s Theory
Isotopes are atoms of the same element that have the same number of protons (that defines the element!), but different numbers of neutrons. This means they have the same atomic number but different mass numbers (protons + neutrons). For example, take carbon (C). Most carbon atoms have 6 protons and 6 neutrons, giving it a mass number of 12 (¹²C).
However, some carbon atoms have 6 protons and 7 neutrons, making their mass number 13 (¹³C). These are both isotopes of carbon – ¹²C and ¹³C. The existence of these different isotopes directly contradicts Dalton’s idea of identical atoms for a single element. Another example is hydrogen; it has isotopes like protium (¹H), deuterium (²H), and tritium (³H), each with a different number of neutrons.
These isotopes show us that atoms of the same element aren’t always identical in mass.
Visual Representation of Isotope Mass Differences
Imagine two circles, both representing carbon atoms. One circle is slightly larger than the other. The smaller circle represents ¹²C (6 protons and 6 neutrons). The larger circle represents ¹³C (6 protons and 7 neutrons). The difference in size visually represents the difference in mass due to that extra neutron in ¹³C.
While the number of protons remains the same (defining them both as carbon), the added neutron increases the overall mass of the atom, demonstrating the limitations of Dalton’s theory which assumed all atoms of the same element had the same mass. This simple visual illustrates how isotopes challenge the core concept of Dalton’s atomic theory.
Chemical Reactions and Atomic Theory
Dalton’s atomic theory, despite its limitations, revolutionized our understanding of chemical reactions. It provided a framework for interpreting experimental observations and paved the way for the more sophisticated models we use today. This section explores how Dalton’s theory both successfully explained and failed to fully account for the intricacies of chemical reactions.
Dalton’s Atomic Theory and Chemical Reactions: Strengths
Dalton’s theory elegantly explained the Law of Conservation of Mass and the Law of Definite Proportions. The Law of Conservation of Mass states that matter cannot be created or destroyed in a chemical reaction; the total mass of the reactants equals the total mass of the products. Dalton’s model, with its indivisible atoms rearranging during reactions, directly supported this.
For example, in the reaction between hydrogen and oxygen to form water (2H₂ + O₂ → 2H₂O), the total mass of hydrogen and oxygen before the reaction equals the mass of water produced. The Law of Definite Proportions states that a given compound always contains the same proportion of elements by mass. Dalton’s model explained this by proposing that compounds are formed by specific combinations of atoms in fixed ratios.
For instance, water always has a 2:1 ratio of hydrogen to oxygen atoms.
A simple diagram illustrating the rearrangement of atoms in the synthesis of water could show two diatomic hydrogen molecules (H₂) and one diatomic oxygen molecule (O₂) combining to form two water molecules (H₂O). Each hydrogen atom is represented as a small circle, and each oxygen atom as a larger circle.
The diagram would visually depict the breaking of the hydrogen-hydrogen and oxygen-oxygen bonds and the formation of new hydrogen-oxygen bonds.
Dalton’s Atomic Theory and Chemical Reactions: Weaknesses
Despite its successes, Dalton’s theory had significant limitations. His assertion that atoms were indivisible was proven incorrect by the discovery of subatomic particles like electrons, protons, and neutrons. This also explained the existence of isotopes, atoms of the same element with different numbers of neutrons, leading to fractional atomic weights. Dalton’s model couldn’t account for isotopes, which are crucial in understanding variations in the properties of elements and their behavior in reactions.
For example, chlorine has two main isotopes, ³⁵Cl and ³⁷Cl, with different masses. This explains why the atomic weight of chlorine is not a whole number. Additionally, Dalton’s theory couldn’t explain why some reactions involved energy changes or the role of electrons in bonding.
Comparison of Dalton’s and Modern Atomic Theories
| Aspect | Dalton’s Model | Modern Atomic Theory |
|---|---|---|
| Nature of Atoms | Indivisible, solid spheres | Complex structures with subatomic particles (protons, neutrons, electrons) |
| Role of Electrons in Bonding | Absent; no explanation of bonding | Crucial role in chemical bonding through electron transfer (ionic) or sharing (covalent) |
| Explanation of Chemical Reactions | Rearrangement of atoms | Rearrangement of atoms driven by electron interactions |
| Handling of Isotopes | Unable to explain their existence | Incorporates isotopes and their influence on atomic mass and properties |
Electron Transfer Reactions
Redox reactions, like the reaction between sodium (Na) and chlorine (Cl), exemplify electron transfer. Sodium readily loses one electron to achieve a stable electron configuration, forming a positively charged sodium ion (Na⁺). Chlorine readily gains one electron to achieve a stable configuration, forming a negatively charged chloride ion (Cl⁻). The electrostatic attraction between Na⁺ and Cl⁻ forms the ionic compound sodium chloride (NaCl).
Lewis dot structures can illustrate this: Na • + :Cl• → Na⁺ + :Cl:⁻.
Electron Sharing Reactions
Covalent bonding, seen in the formation of water (H₂O), involves electron sharing. Each hydrogen atom shares its single electron with the oxygen atom, which shares two electrons, one with each hydrogen. This forms two covalent bonds, resulting in a stable water molecule. Lewis dot structures would show H• + •H + :Ö: → H-Ö-H.
Combustion of Methane: A Comparative Example
The combustion of methane (CH₄) provides a clear comparison between Dalton’s and modern models.A flowchart could depict the following:
1. Balanced Chemical Equation
CH₄ + 2O₂ → CO₂ + 2H₂O
2. Dalton’s Model
The diagram shows one methane molecule and two oxygen molecules rearranging to form one carbon dioxide molecule and two water molecules. The limitation is that it doesn’t show the electron interactions driving the reaction.
3. Modern Model
Lewis dot structures illustrate the breaking of covalent bonds in methane and oxygen and the formation of new covalent bonds in carbon dioxide and water. Electrons are shared to form stable molecules. The reaction involves oxidation of carbon and hydrogen and reduction of oxygen.
4. Comparison
Dalton’s model accurately depicts the rearrangement of atoms but lacks the explanation of electron interactions driving the reaction. The modern model provides a complete picture, including the electron transfer and the energy changes involved.
The Nature of Atoms
Dalton’s idea of atoms as solid, indivisible spheres was, well, kinda cute for its time. Think of it like a super simplified Lego brick – a fundamental building block, but without any internal structure. However, as scientific tools improved, the reality of the atom’s complexity became undeniable, shattering Dalton’s perfectly simple model.The late 19th and early 20th centuries saw a flurry of experiments that revealed the atom wasn’t indivisible at all.
It was, in fact, a bustling microcosm of even smaller particles, each with its own properties and behavior. These discoveries fundamentally changed our understanding of matter and laid the foundation for modern chemistry and physics.
Experiments Revealing Atomic Substructure
Several key experiments contributed to the unraveling of the atom’s secrets. J.J. Thomson’s cathode ray tube experiments, for instance, demonstrated the existence of negatively charged particles—electrons—much smaller than the atom itself. This experiment showed that atoms could be broken down, contradicting Dalton’s claim. Then came Ernest Rutherford’s gold foil experiment, which used alpha particles (positively charged) to bombard a thin gold foil.
The surprising scattering pattern of the alpha particles led to the discovery of the dense, positively charged nucleus at the atom’s center, surrounded by mostly empty space where the electrons resided. These findings completely reshaped our understanding of atomic structure. Finally, experiments involving spectroscopy provided further evidence about the energy levels of electrons within atoms, revealing a more intricate internal structure than previously imagined.
Visual Representation of Atomic Substructure
Imagine a tiny, incredibly dense solar system. At the center is the nucleus, a tiny but massive sphere containing protons (positively charged) and neutrons (neutral charge). These protons and neutrons are tightly packed together, contributing almost all of the atom’s mass. Surrounding the nucleus are electrons, tiny negatively charged particles, whizzing around in specific energy levels or shells, like planets orbiting a star.
The electrons are much lighter than protons and neutrons and occupy a much larger volume compared to the nucleus. The space between the nucleus and the electrons is mostly empty. This model, while still a simplification, provides a more accurate picture of the atom than Dalton’s original indivisible sphere. The size difference between the nucleus and the electron cloud is vast; if the nucleus were the size of a marble, the electrons would be orbiting kilometers away.
This vast empty space is a crucial aspect of atomic structure, explaining many chemical and physical properties.
Dalton’s Model and Nuclear Reactions
Dalton’s atomic theory, while revolutionary for its time, couldn’t explain phenomena discovered later, particularly in the realm of nuclear physics. His model envisioned atoms as indivisible, solid spheres, a picture that completely breaks down when we consider the incredible energies involved in nuclear reactions. The limitations become strikingly apparent when we examine processes like fission and fusion.The discovery of radioactivity, with its emission of alpha, beta, and gamma rays, completely shattered the notion of an unchanging, indestructible atom.
Radioactive decay, where atoms spontaneously transform into different elements, directly contradicts Dalton’s idea of atomic stability. This instability, and the resulting release of tremendous energy, is simply not accounted for in Dalton’s simple model.
Radioactive Decay and Atomic Transmutation
Radioactive decay demonstrates the inherent instability of certain atomic nuclei. For instance, Uranium-238 undergoes alpha decay, emitting an alpha particle (two protons and two neutrons) and transforming into Thorium-234. This is a fundamental change in the atom’s identity, something Dalton’s theory couldn’t explain. His model suggested atoms were unchanging, yet here we see atoms spontaneously changing into entirely different elements, releasing energy in the process.
Another example is the beta decay of Carbon-14, where a neutron transforms into a proton, emitting an electron (beta particle) and an antineutrino. This alters the atomic number, changing carbon into nitrogen. These transformations are impossible to reconcile with Dalton’s indivisible, solid sphere model.
Nuclear Fission and Fusion
Nuclear fission, the splitting of a heavy atomic nucleus into lighter nuclei, releases enormous amounts of energy. The classic example is the fission of Uranium-235, where a neutron bombardment causes the nucleus to split, releasing more neutrons and smaller atoms like Barium and Krypton. This process, with its massive energy release and transformation of elements, directly contradicts Dalton’s concept of the atom’s unchangeability and indivisibility.
Similarly, nuclear fusion, the combining of light atomic nuclei to form heavier ones, also generates immense energy. The sun’s energy is a prime example, where hydrogen nuclei fuse to form helium, releasing energy in the process. Again, Dalton’s model, with its unchanging atoms, provides no mechanism for such transformations and energy release. The immense energies involved in these processes—far exceeding chemical reaction energies—demonstrate the limitations of Dalton’s model.
The Role of Electrons in Bonding
Dalton’s atomic theory, while revolutionary for its time, had significant limitations, particularly concerning the nature of chemical bonding. His model, envisioning atoms as indivisible solid spheres, couldn’t explain the forces holding atoms together in molecules or the diverse properties of different compounds. Understanding the role of electrons in bonding was crucial in resolving these shortcomings and developing a more comprehensive understanding of chemistry.
Dalton’s Atomic Theory Limitations
Dalton’s simple model, while groundbreaking, couldn’t account for the complex behavior of atoms in chemical reactions. Several key shortcomings directly prevented it from explaining chemical bond formation.
| Shortcoming | Explanation | Supporting Evidence |
|---|---|---|
| Atoms are indivisible | Dalton’s theory didn’t acknowledge the existence of subatomic particles like electrons, protons, and neutrons. This prevented an understanding of how electrons interact to form bonds. | J.J. Thomson’s discovery of the electron in 1897, using cathode ray tubes, demonstrated that atoms were divisible and contained negatively charged particles. (Thomson, J.J. (1897). Cathode rays.
|
| All atoms of an element are identical | This ignores the existence of isotopes, atoms of the same element with different numbers of neutrons. This impacts bonding because isotopes have slightly different masses and can affect molecular properties. | The discovery of isotopes, such as different isotopes of chlorine (35Cl and 37Cl), through mass spectrometry experiments, disproved this aspect of Dalton’s theory. (Aston, F. W. (1919). Isotopes*. London Dalton’s atomic theory, groundbreaking for its time, ultimately fell short due to limitations in available technology and understanding. The inherent flaws stem from a reliance on what was then considered a logical interpretation based on prior knowledge and experience , leading to inaccuracies like the assumption of indivisible atoms. Subsequent discoveries, such as subatomic particles, directly contradicted his postulates, highlighting the dynamic nature of scientific understanding and the inherent revisability of even foundational theories. Edward Arnold.) |
| Atoms combine in simple whole-number ratios | While this is often true, it doesn’t account for the complexities of bonding, such as polyatomic ions and molecules with varying bond orders. | The existence of polyatomic ions like sulfate (SO42-) and complex molecules like benzene (C 6H 6) demonstrate that bonding is more intricate than simple whole-number ratios suggest. The discovery of these structures came from advancements in spectroscopy and X-ray crystallography. (Kekulé, F. A. (1865).
|
Dalton’s model failed to predict isotopes because it assumed all atoms of an element were identical. The discovery of isotopes showed that atoms of the same element can have different masses due to varying numbers of neutrons. This impacted the understanding of bonding because the slightly different masses of isotopes can affect the vibrational frequencies and other properties of molecules, although the chemical behavior remains largely unchanged.
Ionic and Covalent Bonding
Ionic and covalent bonds are two primary types of chemical bonds, differing in how atoms share or transfer electrons. Electronegativity, the ability of an atom to attract electrons in a chemical bond, plays a crucial role in determining which type of bond forms.Ionic bonding involves the complete transfer of electrons from one atom to another, resulting in the formation of ions (charged atoms).
For example, in the formation of sodium chloride (NaCl), sodium (Na) loses one electron to become a positively charged Na + ion, while chlorine (Cl) gains one electron to become a negatively charged Cl – ion. The electrostatic attraction between these oppositely charged ions forms the ionic bond. A simple diagram would show a sodium atom with one valence electron transferring that electron to a chlorine atom with seven valence electrons, resulting in Na + and Cl – ions.Covalent bonding involves the sharing of electrons between atoms.
In a covalent bond, atoms share one or more pairs of electrons to achieve a stable electron configuration, often resembling a noble gas. For example, in a molecule of hydrogen (H 2), each hydrogen atom shares its single electron with the other, resulting in a shared electron pair that holds the atoms together. A diagram would show two hydrogen atoms, each with one electron, overlapping their electron orbitals to form a shared electron pair.Electronegativity differences between atoms determine the type of bond.
A large electronegativity difference leads to ionic bonding, while a small difference results in covalent bonding. Bonds with intermediate electronegativity differences are polar covalent bonds.
| Property | Ionic Bond | Covalent Bond |
|---|---|---|
| Bond Strength | Generally strong | Variable, can be strong or weak |
| Melting/Boiling Points | High | Variable, can be low or high |
| Electrical Conductivity (Solid) | Poor | Poor (except for graphite) |
| Electrical Conductivity (Molten) | Good | Poor |
| Solubility in Polar Solvents | Generally good | Variable, depends on polarity |
| Solubility in Nonpolar Solvents | Poor | Generally good if nonpolar |
Polar covalent bonds occur when the electrons are shared unequally between atoms due to a difference in electronegativity. This creates a partial positive charge (δ+) on the less electronegative atom and a partial negative charge (δ-) on the more electronegative atom. Water (H 2O), hydrogen fluoride (HF), and ammonia (NH 3) are examples of molecules with polar covalent bonds.
In water, oxygen is more electronegative than hydrogen, resulting in a dipole moment with the oxygen atom carrying a partial negative charge and the hydrogen atoms carrying partial positive charges. Dipole moment vectors would point from the positive hydrogen atoms towards the negative oxygen atom.
Dalton’s Model vs. Experimental Observations
Dalton’s model predicted that the mass ratios in chemical compounds would always be simple whole numbers, reflecting the ratios of atoms combining. However, mass spectrometry data often reveals more complex ratios due to the existence of isotopes. For example, chlorine’s atomic mass is approximately 35.5 amu, not a whole number, because it is a mixture of 35Cl and 37Cl isotopes.
This discrepancy highlights a limitation of Dalton’s indivisible atom concept.The discovery of the electron (Thomson, 1897) revolutionized atomic theory. Subsequent discoveries, such as the nucleus (Rutherford, 1911) and the Bohr model (Bohr, 1913), provided a more accurate representation of the atom, including the arrangement of electrons and their role in bonding.A brief timeline:* 1897: Discovery of the electron by J.J.
Thomson.
1911
Discovery of the atomic nucleus by Ernest Rutherford.
1913
Niels Bohr proposes the Bohr model of the atom.These advancements resolved the limitations of Dalton’s model by incorporating subatomic particles and explaining the behavior of electrons in chemical bonding. The Bohr model, although simplistic, provided a framework for understanding how electrons occupy specific energy levels and participate in bonding.
Limitations of Simple Lewis Dot Structures
Simple Lewis dot structures, while useful for representing many molecules, fail to accurately depict molecules with resonance structures. Resonance occurs when a molecule can be represented by multiple Lewis structures that differ only in the placement of electrons. Benzene (C 6H 6) and ozone (O 3) are examples. Benzene’s structure is represented by two resonance structures showing alternating single and double bonds between carbon atoms.
The actual structure is a hybrid of these two, with bond lengths intermediate between single and double bonds. This delocalization of electrons affects the bond order (the number of bonds between two atoms) and overall stability of the molecule. Ozone also exhibits resonance, with the double bond shifting between the two oxygen-oxygen bonds. The true structure is a resonance hybrid with a bond order of 1.5 for each oxygen-oxygen bond.
Quantum Mechanics and Atomic Structure
Yo Jogja! We’ve talked about Dalton’s atomic theory, but it’s, like,way* outdated. Think of it as a cassette tape in a Spotify world. Quantum mechanics totally revolutionized our understanding of atoms, revealing a level of complexity Dalton couldn’t even dream of. Let’s dive into how the quantum world blows Dalton’s model out of the water.
Limitations of Dalton’s Model in Light of Quantum Mechanics
Dalton’s theory, while groundbreaking for its time, had some serious flaws when compared to the more nuanced understanding provided by quantum mechanics. His idea of atoms as solid, indivisible spheres just doesn’t cut it when we consider the existence of subatomic particles and isotopes. Isotopes, atoms of the same element with differing neutron numbers, directly contradict Dalton’s concept of all atoms of an element being identical.
The discovery of electrons, protons, and neutrons shattered the “indivisible” part of his theory. Furthermore, Dalton’s model couldn’t explain the intricate dance of electrons during chemical reactions or the quantized nature of energy absorption and emission. Atomic spectra, the unique patterns of light emitted by elements, provide clear evidence of this quantized energy, a phenomenon completely outside the scope of Dalton’s simple model.
Think of it like trying to explain a symphony with only a single drum – you’re missing a whole lot of the music!
Electron Orbitals and Their Contradiction of Dalton’s Model
Electron orbitals represent a fundamental shift from Dalton’s view. Instead of solid spheres, quantum mechanics describes electrons as existing in regions of probability, called orbitals. These orbitals aren’t neat, well-defined paths like planets orbiting a sun; they’re fuzzy clouds representing the likelihood of finding an electron in a particular area. The Heisenberg Uncertainty Principle further complicates things, stating that we can’t simultaneously know both an electron’s position and momentum with perfect accuracy.
This inherent uncertainty directly challenges Dalton’s image of a precisely defined, solid atom.The different types of orbitals (s, p, d, f) have distinct shapes and can hold varying numbers of electrons.
| Orbital Type | Shape | Orbitals per Subshell | Maximum Electrons |
|---|---|---|---|
| s | Spherical | 1 | 2 |
| p | Dumbbell | 3 | 6 |
| d | Complex | 5 | 10 |
| f | Very Complex | 7 | 14 |
The existence of these orbitals, with their probabilistic nature and internal structure, directly contradicts Dalton’s idea of a solid, indivisible atom. Classical physics, which Dalton’s model implicitly relies on, fails miserably to describe electron behavior at the atomic level. Classical physics predicts electrons would spiral into the nucleus, collapsing the atom – something we clearly don’t observe. Quantum mechanics, however, elegantly explains the stability of atoms and the intricacies of electron behavior.
Conceptual Diagram: Dalton’s Model vs. Quantum Mechanical Model
Imagine Dalton’s model as a simple, solid, red billiard ball. That’s it. No internal structure, just a single, uniform entity. Now, picture the quantum mechanical model. It’s a much more complex image, showing a tiny, dense nucleus (containing protons and neutrons) at the center, surrounded by a cloud of probability representing the electrons in various orbitals.
The cloud isn’t uniform; its density varies depending on the probability of finding an electron in a given location. The different orbitals are represented by different regions within the cloud, some spherical (s orbitals), some dumbbell-shaped (p orbitals), and others with even more complex geometries.It’s crucial to understand that a simple visual model can only provide a limited representation of the quantum mechanical atom.
The probabilistic nature of electron location makes it impossible to create a truly accurate visual depiction. The “electron cloud” concept is a helpful simplification, but it’s important to remember that it’s a representation of probability, not a physical cloud of matter.
The Evolution of Atomic Models
The understanding of the atom has undergone a dramatic transformation over centuries, evolving from a simple, indivisible sphere to the complex, probabilistic model we know today. This evolution is marked by groundbreaking experiments and the insightful contributions of numerous scientists, each building upon the work of their predecessors. This section will explore the key milestones in this fascinating journey, highlighting the experimental evidence and theoretical reasoning behind each major shift in our understanding of atomic structure.
Timeline of Atomic Models
The development of atomic models can be visualized as a progression, each model refining our understanding based on new experimental findings. The following table Artikels the key models and their development over time.
| Year | Scientist(s) | Model Name | Key Features of the Model | Significant Experiments/Discoveries |
|---|---|---|---|---|
| ~1803 | John Dalton | Solid Sphere Model | Atoms are indivisible, solid spheres with unique properties for each element. All atoms of a given element are identical. | Dalton’s Law of Partial Pressures, Law of Multiple Proportions |
| 1897 | J.J. Thomson | Plum Pudding Model | Atoms are composed of a positively charged sphere with negatively charged electrons embedded within it. | Discovery of the electron through cathode ray tube experiments. |
| 1911 | Ernest Rutherford | Nuclear Model | Atoms consist of a small, dense, positively charged nucleus surrounded by mostly empty space containing orbiting electrons. | Gold foil experiment demonstrating the existence of a nucleus. |
| 1913 | Niels Bohr | Bohr Model | Electrons orbit the nucleus in specific energy levels or shells. Electrons can jump between energy levels by absorbing or emitting photons. | Explanation of atomic spectra (emission and absorption lines) |
| 1920s-Present | Various Scientists (Schrödinger, Heisenberg, etc.) | Quantum Mechanical Model | Electrons exist in orbitals, regions of space where the probability of finding an electron is high. The exact location and momentum of an electron cannot be simultaneously determined (Heisenberg Uncertainty Principle). | Development of quantum mechanics, wave-particle duality of electrons. |
Experiments and Discoveries Leading to Model Shifts
Several crucial experiments significantly impacted our understanding of the atom, prompting the development of new models.
| Experiment Name | Scientist(s) | Year | Methodology | Results | Impact on Atomic Theory |
|---|---|---|---|---|---|
| Cathode Ray Tube Experiment | J.J. Thomson | 1897 | High voltage applied across a vacuum tube; deflection of the ray by electric and magnetic fields observed. | Discovery of negatively charged particles (electrons); determined charge-to-mass ratio. | Challenged Dalton’s indivisible atom; led to the plum pudding model. |
| Gold Foil Experiment | Ernest Rutherford | 1911 | Alpha particles bombarded a thin gold foil; scattering of particles observed. | Most particles passed through; some were deflected at large angles, indicating a concentrated positive charge (nucleus). | Disproved the plum pudding model; led to the nuclear model. |
| Atomic Spectra Experiments | Various Scientists | Late 19th and early 20th centuries | Analysis of light emitted by excited atoms. | Discrete lines observed, not continuous spectrum; specific wavelengths for each element. | Could not be explained by the nuclear model; led to the Bohr model. |
Contributions of Key Scientists and Limitations of Their Models
Each scientist’s contribution built upon previous work, addressing limitations and refining our understanding.John Dalton’s solid sphere model, while a crucial first step, failed to account for the existence of subatomic particles. J.J. Thomson’s plum pudding model, though incorporating electrons, couldn’t explain the results of Rutherford’s gold foil experiment. Rutherford’s nuclear model, while revolutionary, couldn’t explain the stability of atoms or the discrete nature of atomic spectra.
Bohr’s model addressed the spectral lines but ultimately failed to accurately describe atoms with more than one electron.
Comparative Analysis of Thomson, Rutherford, and Bohr Models
Thomson’s model introduced the electron, a subatomic particle, moving away from Dalton’s indivisible atom. Rutherford’s model further refined this by introducing the concept of a nucleus, a dense, positively charged center. Bohr improved upon Rutherford’s model by incorporating quantized energy levels for electrons, explaining the discrete nature of atomic spectra. However, Bohr’s model still relied on classical physics concepts, which were ultimately insufficient.
Dalton’s atomic theory, a cornerstone of early chemistry, suffers from limitations revealed by later discoveries; for instance, the indivisibility of the atom is now demonstrably false. Understanding this requires clarifying the fundamental difference between a theory and a hypothesis, a distinction explored in detail at which of the following distinguishes a theory from a hypothesis.
This distinction highlights why some of Dalton’s postulates, while groundbreaking for their time, are now considered incomplete representations of atomic structure.
Quantum Mechanical Model Deep Dive
The quantum mechanical model revolutionized our understanding of atomic structure. It describes electrons not as particles orbiting the nucleus in fixed paths, but as existing in orbitals—regions of space where the probability of finding an electron is high. This probability is described by wave functions, solutions to the Schrödinger equation. The model incorporates quantum numbers: the principal quantum number (n) determines the energy level, the azimuthal quantum number (l) determines the shape of the orbital, the magnetic quantum number (ml) determines the orientation of the orbital in space, and the spin quantum number (ms) describes the intrinsic angular momentum of the electron.
The Heisenberg Uncertainty Principle states that it is impossible to simultaneously know both the position and momentum of an electron with perfect accuracy. The wave-particle duality of electrons means that they exhibit properties of both waves and particles, further complicating the classical picture. A simplified explanation of the Schrödinger equation is beyond the scope of this section, but it’s fundamentally a mathematical description of the electron’s wave function, allowing us to calculate the probability of finding an electron in a particular region of space.
Dalton’s Contributions Despite Inaccuracies
John Dalton’s atomic theory, while revolutionary for its time, contained inaccuracies that were later corrected by advancements in scientific understanding and technology. However, his contributions remain foundational to modern chemistry, highlighting the iterative nature of scientific progress where even imperfect models can pave the way for significant breakthroughs. This analysis will delve into the specific inaccuracies of Dalton’s model, explore its significant contributions despite these limitations, and examine its lasting impact on the field.
Specific Inaccuracies in Dalton’s Atomic Theory
Dalton’s atomic theory, proposed in the early 1800s, made several assumptions that proved inaccurate with subsequent discoveries. These inaccuracies stemmed from limitations in the available technology and understanding of the atom’s internal structure.
| Inaccuracy | Explanation | Impact on Later Theories |
|---|---|---|
| Atoms of the same element are identical in mass and properties. | This ignores the existence of isotopes, atoms of the same element with differing numbers of neutrons and thus, different masses. | Led to the development of the concept of isotopes and the refinement of atomic mass calculations. |
| Atoms are indivisible and indestructible. | This fails to account for subatomic particles like protons, neutrons, and electrons, which were discovered later. Atoms can be split through nuclear reactions. | The discovery of subatomic particles revolutionized atomic theory, leading to models like the Rutherford model and the Bohr model. |
| Atoms of different elements combine in simple whole-number ratios to form compounds. | While generally true for many compounds, this doesn’t account for complex molecules or compounds with variable composition. | This aspect needed refinement to accommodate the complexities of molecular structures and bonding. |
Historical Context of Dalton’s Inaccuracies
Dalton’s work was built upon the burgeoning field of chemistry at the time. The lack of sophisticated instruments like mass spectrometers prevented the detection of isotopes. Furthermore, the concept of subatomic particles was entirely unknown. Dalton’s model, therefore, represented the best understanding possible given the technological and theoretical limitations of his era. His reliance on experimental observations, primarily focusing on gas behavior and chemical reactions, naturally led to a simplified view of the atom.
Significant Contributions Despite Inaccuracies
Despite its inaccuracies, Dalton’s atomic theory made significant contributions to the advancement of chemistry.
Dalton’s Law of Multiple Proportions
Dalton’s Law of Multiple Proportions states that when two elements combine to form more than one compound, the masses of one element that combine with a fixed mass of the other element are in a ratio of small whole numbers. For example, carbon and oxygen can form carbon monoxide (CO) and carbon dioxide (CO₂). The ratio of oxygen masses combining with a fixed mass of carbon is 1:2, reflecting the simple whole-number ratio of oxygen atoms in the two compounds.
This law provided crucial quantitative support for the atomic theory.
Dalton’s Contribution to the Law of Conservation of Mass
Dalton’s work strongly supported the Law of Conservation of Mass, which states that mass is neither created nor destroyed in a chemical reaction. While Lavoisier is credited with establishing this law through meticulous experimentation, Dalton’s atomic theory provided a theoretical framework explaining
why* mass is conserved
atoms rearrange during reactions but are neither created nor destroyed. This offered a deeper, more fundamental understanding than Lavoisier’s empirical observations alone.
Foundation for Future Advancements in Chemistry
- Dalton’s theory provided the fundamental concept of the atom as the basic building block of matter, a concept that remains central to chemistry.
- It introduced the idea of relative atomic masses, although the values were initially inaccurate, setting the stage for the development of precise atomic mass measurements.
- It established a quantitative basis for chemical reactions, enabling the development of stoichiometry and other quantitative aspects of chemistry.
Impact on the Periodic Table
Dalton’s work, specifically his concept of relative atomic masses, although imperfect, was crucial for the later development of the periodic table. Mendeleev, in developing his periodic table, used atomic weights (which were closely related to Dalton’s relative atomic masses) as a primary organizing principle. While Mendeleev’s periodic table relied on more sophisticated data than Dalton initially had access to, Dalton’s conceptual framework of relative atomic masses provided a foundation for this monumental achievement.
Lasting Impact and Examples
Dalton’s legacy extends far beyond his initial atomic model.
Specific Examples of Dalton’s Lasting Impact
Stoichiometry
The ability to quantitatively predict the amounts of reactants and products in chemical reactions is directly based on the concept of atoms combining in fixed ratios, a core idea in Dalton’s theory.
Chemical Analysis
Many analytical techniques used to determine the composition of substances rely on the principles of atomic masses and ratios, which were first conceptualized by Dalton.
Molecular Formulas
The determination of molecular formulas, crucial for understanding the structure and properties of compounds, is fundamentally linked to Dalton’s concept of atoms combining in whole-number ratios.
Modern Relevance of Dalton’s Contributions
Dalton’s contributions remain relevant in modern chemistry. The concept of atoms combining in fixed ratios is fundamental to all chemical calculations and understanding. His work laid the groundwork for advancements in fields like materials science, biochemistry, and nanotechnology, where understanding the behavior of atoms and molecules is paramount.
Further Research Avenues
- A detailed historical analysis of the reception and critique of Dalton’s theory within the scientific community of his time.
- An investigation into the specific technological advancements that allowed for the identification and characterization of isotopes and subatomic particles.
- A comparative study of Dalton’s influence on the development of the periodic table in different national scientific communities.
The Law of Multiple Proportions
Yo, Jogja peeps! Let’s dive into Dalton’s Law of Multiple Proportions. It’s a pretty crucial part of his atomic theory, but like, not everything is perfect, right? This law basically says that when two elements form more than one compound, the ratios of the masses of the second element that combine with a fixed mass of the first element will always be ratios of small whole numbers.
Think of it as a recipe – you can have different ratios of ingredients, but they’ll always be in simple, whole number ratios. This supported Dalton’s idea that elements combine in whole number ratios of atoms.This law was a big deal back in the day because it helped scientists understand how elements combine to form different compounds. It gave more credence to the idea that matter is made up of atoms and that these atoms combine in specific, predictable ways.
However, it’s not a universal truth applicable to
all* chemical reactions.
Limitations of the Law of Multiple Proportions
The Law of Multiple Proportions, while a significant step forward, has its limitations. It doesn’t always perfectly describe the behavior of all chemical reactions, especially those involving complex compounds or those that don’t involve simple whole-number ratios of atoms. For example, the law struggles with reactions involving polyatomic ions or those with variable oxidation states, which can lead to non-whole number ratios.
Furthermore, some compounds exhibit non-stoichiometric compositions, meaning their ratios aren’t perfectly fixed and deviate from simple whole numbers. This happens in certain solid-state compounds and alloys where there are defects in the crystal structure.
Examples Supporting and Challenging the Law
Let’s look at some examples. Carbon monoxide (CO) and carbon dioxide (CO2) perfectly illustrate the law. In CO, the ratio of oxygen to carbon is approximately 1:1, while in CO2, it’s approximately 2:1 – a simple whole-number ratio. This supports Dalton’s theory beautifully.However, consider non-stoichiometric compounds like wustite (iron(II) oxide), often represented as FeO. In reality, the iron to oxygen ratio isn’t exactly 1:1; it varies slightly due to defects in the crystal lattice, falling outside the neat whole-number ratio predicted by the Law of Multiple Proportions.
This shows a limitation of the law when dealing with the complexities of real-world materials. Another example is the formation of alloys, where the ratios of constituent metals are not always simple whole numbers.
Dalton’s Law of Partial Pressures
Dalton’s Law of Partial Pressures, a cornerstone of gas behavior understanding, significantly intersects with his atomic theory. While not directly proving his atomic postulates, it provided supporting evidence and highlighted some of the theory’s inherent limitations. This exploration delves into the law’s definition, relevance to atomic theory, and its enduring impact on scientific understanding.
Mathematical Definition of Dalton’s Law of Partial Pressures
Dalton’s Law of Partial Pressures states that the total pressure exerted by a mixture of non-reacting gases is equal to the sum of the partial pressures of the individual gases. Mathematically, this is represented as:
Ptotal = P 1 + P 2 + P 3 + … + P n
where P total is the total pressure and P 1, P 2, P 3,… P n are the partial pressures of each gas in the mixture. A partial pressure represents the hypothetical pressure that a gas would exert if it alone occupied the entire volume.
Illustrative Example of Dalton’s Law
Imagine a container holding three gases: oxygen (O 2), nitrogen (N 2), and carbon dioxide (CO 2). The partial pressure of oxygen is 2 atm, nitrogen is 3 atm, and carbon dioxide is 1 atm. A simple diagram could depict three separate compartments, each representing one gas with its partial pressure labeled. Then, a combined compartment shows all three gases mixed.[Diagram description: Three separate boxes are shown, labeled “O2 (2 atm)”, “N2 (3 atm)”, and “CO2 (1 atm)”.
Arrows point to a fourth, larger box labeled “Mixture (6 atm)” representing the combined gases. ]According to Dalton’s Law, the total pressure in the container would be 2 atm + 3 atm + 1 atm = 6 atm.
Underlying Assumptions of Dalton’s Law, Why are some of dalton’s theories not true
Dalton’s Law relies on several key assumptions. Firstly, the gases in the mixture must be non-reactive; they should not chemically interact with each other. Secondly, the gases should ideally behave ideally – meaning their intermolecular forces are negligible, and their volume is insignificant compared to the container volume. These conditions are most closely approximated at low pressures and high temperatures.
Dalton’s Law and its Relation to Atomic Theory
Dalton’s Law supported his atomic theory indirectly. The fact that pressures added linearly suggested that individual gas particles (atoms, according to Dalton) exerted independent pressures, not interacting significantly with each other. This aligns with his postulate of indivisible atoms. The law also indirectly supported the idea that chemical reactions involved the combination or separation of atoms, as the behavior of gas mixtures reflected the independent behavior of constituent atoms.
Limitations of Dalton’s Atomic Theory and its Impact on the Law of Partial Pressures
Dalton’s atomic theory was limited by its assumption of indivisible atoms. The discovery of subatomic particles like electrons, protons, and neutrons later proved this assumption incorrect. This didn’t invalidate Dalton’s Law of Partial Pressures directly. However, a more accurate understanding of atomic structure helps explain why ideal gas behavior (a key assumption of Dalton’s Law) breaks down at high pressures or low temperatures, where intermolecular forces become significant.
Comparison of Dalton’s Understanding of Gases with the Kinetic Theory
Dalton’s model lacked the dynamic aspect of the kinetic theory of gases. Dalton’s understanding implied a static picture of gas particles. The kinetic theory, on the other hand, describes gases as a collection of constantly moving particles whose collisions contribute to pressure. The kinetic theory provides a more complete and accurate explanation of gas behavior, including deviations from ideality.
Inaccuracies in Dalton’s Atomic Theory and their Impact on the Law of Partial Pressures
Two significant inaccuracies were: (1) The assumption that all atoms of an element are identical in mass and properties (Isotopes were later discovered), and (2) the assumption that atoms of different elements differ significantly in mass and properties. While these inaccuracies don’t directly affect the validity of Dalton’s Law of Partial Pressures at the macroscopic level (as it deals with bulk properties), they highlight that the underlying microscopic picture is more complex than Dalton envisioned.
The law remains accurate for many practical applications even with these inaccuracies.
Experimental Results Contradicting Dalton’s Law and their Explanations
At the time, significant deviations from Dalton’s Law were not widely observed under typical experimental conditions. Deviations became apparent with more precise measurements at higher pressures and lower temperatures, which were explained later by the van der Waals equation, which accounts for intermolecular forces and the finite volume of gas particles.
Practical Applications of Dalton’s Law of Partial Pressures
Dalton’s Law has wide-ranging applications. In scuba diving, it helps calculate the partial pressures of different gases in the air tank to avoid decompression sickness. In atmospheric science, it is used to analyze the composition of the atmosphere, determining the partial pressure of oxygen, nitrogen, and other gases at various altitudes.
Contribution to Understanding Gas Mixtures
Dalton’s Law provides a fundamental framework for understanding gas mixtures in various contexts. Respiration, for instance, involves the partial pressures of oxygen and carbon dioxide in the lungs and blood. Industrial processes like the Haber-Bosch process for ammonia synthesis involve carefully controlling the partial pressures of reactants to optimize yield.
Comparison with Other Gas Laws
Dalton’s Law complements other gas laws like Boyle’s Law (pressure-volume relationship at constant temperature) and Charles’s Law (volume-temperature relationship at constant pressure). While Boyle’s and Charles’s laws deal with single gases, Dalton’s Law extends this to mixtures, providing a more comprehensive understanding of gas behavior.
Summary Table
| Aspect | Description | Relevance to Dalton’s Atomic Theory |
|---|---|---|
| Dalton’s Law (Mathematical) | Ptotal = P1 + P2 + P3 + … + Pn | Supports the idea of independent behavior of gas particles (atoms, according to Dalton). |
| Underlying Assumptions | Non-reactive gases, ideal gas behavior (low pressure, high temperature). | Implies a simplified model of atomic interactions. |
| Limitations of the Law | Deviations from ideality at high pressure or low temperature. | Highlights limitations of Dalton’s simplified atomic model. |
| Practical Applications | Scuba diving calculations, atmospheric analysis, industrial process control. | Demonstrates the law’s usefulness despite limitations of the atomic theory. |
Experimental Evidence Against Dalton’s Theory
Dalton’s atomic theory, while revolutionary for its time, made several assumptions that later experimental evidence proved inaccurate. These experiments not only revealed the limitations of Dalton’s model but also paved the way for a more nuanced understanding of atomic structure. The discrepancies discovered highlighted the need for a more sophisticated model that could account for the complexities of the atom.The discovery of subatomic particles and isotopes provided the most significant challenges to Dalton’s postulates.
Specifically, the existence of isotopes directly contradicted Dalton’s assertion that all atoms of a given element are identical in mass and properties. Furthermore, the discovery of electrons, protons, and later neutrons shattered the idea of the atom as an indivisible, solid sphere.
The Discovery of Isotopes
J.J. Thomson’s work with cathode ray tubes in the late 19th century led to the discovery of the electron, a negatively charged subatomic particle. This directly challenged Dalton’s idea of the atom as indivisible. Further experiments, particularly mass spectrometry developed by J.J. Thomson and later refined by F.W.
Aston, provided definitive proof of the existence of isotopes. Mass spectrometry separates ions based on their mass-to-charge ratio. Aston’s work demonstrated that many elements exist as a mixture of atoms with slightly different masses but identical chemical properties. For example, chlorine exists as a mixture of two isotopes, chlorine-35 and chlorine-37, with different numbers of neutrons but the same number of protons and electrons.
This variation in mass contradicted Dalton’s postulate that all atoms of the same element possess identical mass. The observation of different isotopes of the same element directly contradicted Dalton’s theory. This experimental evidence showcased that atoms of the same element could have different masses.
The Discovery of Subatomic Particles
The discovery of the electron by J.J. Thomson, through experiments with cathode ray tubes, was a pivotal moment. These experiments involved passing an electric current through a gas at low pressure within a sealed tube. The resulting beam, known as a cathode ray, was deflected by both electric and magnetic fields, indicating it consisted of negatively charged particles.
Thomson’s measurements allowed him to determine the charge-to-mass ratio of the electron, demonstrating that it was much lighter than the smallest atom known at the time. This clearly demonstrated that atoms were not indivisible, as Dalton proposed, but contained smaller, negatively charged components. The later discovery of protons and neutrons further solidified this understanding. Rutherford’s gold foil experiment, while not directly contradicting Dalton’s indivisibility postulate in the same way, provided further evidence for a complex internal structure of the atom.
It showed that most of the atom’s mass was concentrated in a tiny, positively charged nucleus, leaving the rest of the atom mostly empty space.
Modern Atomic Theory and its Refinements
Yo, Jogja peeps! So, Dalton’s atomic theory was a total game-changer back in the day, right? But, like, science keeps evolving, and our understanding of atoms has gotten way more nuanced since then. Let’s dive into the modern atomic theory – it’s way more complex, but also way cooler.Modern atomic theory builds upon Dalton’s foundational work but incorporates discoveries made over the past century and a half.
It’s less about simple, indivisible spheres and more about complex quantum systems with mind-bending properties. We’re talking subatomic particles, wave-particle duality, and probabilities, man!
Key Principles of Modern Atomic Theory
Modern atomic theory centers on the idea that atoms are composed of a nucleus containing protons and neutrons, surrounded by a cloud of electrons. The number of protons defines the element (atomic number), while the sum of protons and neutrons gives the mass number. Electrons occupy specific energy levels or orbitals, described by quantum numbers, which dictate their behavior and probability distribution.
Isotopes, atoms of the same element with differing neutron numbers, also play a crucial role. This model accurately predicts chemical behavior and explains phenomena like radioactivity and nuclear reactions, something Dalton’s model couldn’t even touch.
Comparison of Modern and Dalton’s Atomic Theories
Dalton’s model pictured atoms as solid, indivisible spheres with identical properties for each element. Modern atomic theory, on the other hand, reveals a much more intricate structure. Dalton’s theory couldn’t account for isotopes, the existence of subatomic particles, or the complexities of chemical bonding. Modern theory elegantly incorporates these aspects, explaining things like the different isotopes of carbon (carbon-12 and carbon-14) and the diverse types of chemical bonds.
Think of it as upgrading from a basic Nokia 3310 to a supercharged smartphone – same basic function (communication), but vastly improved capabilities and complexity.
Ongoing Research and Refinements in Atomic Structure
Research continues to refine our understanding of the atom. Scientists are constantly exploring the behavior of subatomic particles, investigating exotic atoms with unusual compositions, and developing more precise models of electron orbitals. For example, the Standard Model of particle physics describes the fundamental building blocks of matter and their interactions, going far beyond the simple proton-neutron-electron model. The search for new particles and a deeper understanding of the strong and weak nuclear forces remains a key focus in modern physics, constantly refining our comprehension of the atomic realm.
It’s like a never-ending game of atomic Jenga – we keep pulling out pieces, and sometimes find hidden layers, but the tower mostly remains standing, albeit more complex.
FAQs
What specific experiments disproved Dalton’s theory of indivisible atoms?
Experiments like J.J. Thomson’s cathode ray tube experiments revealing the electron and Rutherford’s gold foil experiment demonstrating the nucleus directly contradicted Dalton’s idea of a solid, indivisible atom.
How did Dalton’s Law of Multiple Proportions contribute to his theory, even though it has limitations?
The Law of Multiple Proportions provided strong evidence supporting the concept of atoms combining in fixed ratios, a key aspect of Dalton’s theory. While not universally applicable, it was a significant step towards quantitative chemistry.
What is the significance of isotopes in challenging Dalton’s atomic theory?
The discovery of isotopes showed that atoms of the same element can have different masses, directly contradicting Dalton’s postulate of identical atoms for a given element.
Did Dalton’s work have any lasting positive impacts despite its inaccuracies?
Absolutely! Dalton’s work provided the fundamental framework for understanding chemical reactions and laid the groundwork for the periodic table. His focus on quantitative analysis revolutionized chemistry.


