How many game theories were correct? This question probes the very heart of predictive modeling in fields ranging from economics and political science to biology and computer science. The accuracy of game theory predictions, however, isn’t a simple yes or no answer; instead, it exists on a spectrum, from perfectly accurate quantitative predictions to broadly consistent qualitative trends. This exploration delves into the complexities of validating game theory, examining successful applications alongside notable failures, and considering the role of assumptions, external factors, and the ever-evolving nature of these models.
We will investigate various factors that influence the accuracy of game theory predictions, including the inherent assumptions within different models, the impact of incomplete information and irrational behavior, and the influence of unpredictable external events. Through detailed case studies across diverse disciplines, we will analyze instances where game theory provided remarkably accurate forecasts and those where its predictions fell short.
Ultimately, this exploration aims to provide a nuanced understanding of game theory’s strengths and limitations, highlighting avenues for future refinement and improvement.
Defining “Correct” Game Theory Predictions
The accuracy of game theory predictions, a cornerstone of its practical application, is not a binary concept. Instead, it exists on a spectrum, influenced by various factors including model complexity, data availability, and the inherent unpredictability of human behavior. Understanding this spectrum is crucial for evaluating the usefulness and limitations of game theory in diverse fields.
Spectrum of Correctness Levels for Game Theory Predictions
Assessing the accuracy of game theory predictions requires a nuanced approach, moving beyond simple “correct” or “incorrect” classifications. We propose a five-level spectrum to capture the varying degrees of predictive success:
- Perfectly Accurate: The model precisely predicts both the qualitative and quantitative aspects of the outcome. For example, a perfectly accurate model predicting the exact number of players choosing a specific strategy in a repeated Prisoner’s Dilemma experiment, with a deviation of 0%. Metrics: 0% deviation from predicted outcome, perfect correlation (r=1).
- Highly Accurate: The model accurately predicts qualitative outcomes and quantitative predictions fall within a narrow margin of error (e.g., ±5%). An example would be accurately predicting the winner of an auction but slightly misjudging the final bid price. Metrics: Deviation within ±5% from predicted outcome, high correlation (r > 0.8).
- Moderately Accurate: The model predicts the general trend of the outcome, but with noticeable quantitative deviations (e.g., ±15%). Predicting a general increase in market share for a product, but overestimating the actual increase by 10%, falls into this category. Metrics: Deviation within ±15% from predicted outcome, moderate correlation (0.5 < r ≤ 0.8).
- Broadly Consistent: The model’s predictions align qualitatively with the observed trends, but with significant quantitative discrepancies. For instance, a model correctly predicting a decline in cooperation in a public goods game but significantly underestimating the rate of decline. Metrics: Qualitative alignment, but low correlation (0.3 < r ≤ 0.5) or significant quantitative deviation.
- Inaccurate: The model’s predictions bear little or no resemblance to the observed outcomes. A model predicting a peaceful resolution to a conflict that escalates into war would fall under this category. Metrics: High deviation, low or negative correlation (r ≤ 0.3).
Accuracy Rubric for Evaluating Game Theory Predictions
A structured rubric provides a standardized framework for assessing the accuracy of game theory predictions across various contexts. The rubric below offers a systematic evaluation based on predictive power, contextual appropriateness, and robustness to assumptions.
| Criterion | Excellent (5 points) | Good (4 points) | Fair (3 points) | Poor (2 points) | Unacceptable (1 point) |
|---|---|---|---|---|---|
| Predictive Power | Precisely predicts both qualitative and quantitative outcomes. | Accurately predicts qualitative outcomes; quantitative predictions are within a reasonable margin of error. | Predicts general trends, but with significant quantitative deviations. | Predictions are partially aligned with observed outcomes, with considerable error. | Predictions bear little to no resemblance to observed outcomes. |
| Contextual Appropriateness | Model perfectly accounts for all relevant contextual factors. | Model accounts for most relevant contextual factors. | Model accounts for some relevant contextual factors. | Model fails to account for several relevant contextual factors. | Model ignores crucial contextual factors. |
| Robustness to Assumptions | Predictions remain valid under a wide range of parameter changes. | Predictions are relatively robust to minor changes in assumptions. | Predictions are sensitive to changes in assumptions. | Predictions are highly sensitive to changes in assumptions. | Predictions are invalidated by minor changes in assumptions. |
Challenges of Empirically Verifying Game Theory Predictions
Empirical verification of game theory predictions faces several significant hurdles:
- Data Availability: Real-world data relevant to game-theoretic models is often scarce, incomplete, or unreliable. For instance, obtaining comprehensive data on the strategic interactions between nations during an international crisis is extremely challenging due to information asymmetry and secrecy. Mitigation Strategy: Develop innovative data collection methods, utilize publicly available data sources creatively, and focus on simpler, more easily testable models.
- Model Complexity: Many game-theoretic models are highly complex, making it difficult to isolate the effects of specific variables and to assess the model’s overall predictive power. The complexity of models designed to predict stock market behavior, for instance, often obscures the underlying causal relationships. Mitigation Strategy: Employ sensitivity analysis, develop simplified versions of complex models for initial testing, and focus on testing specific hypotheses derived from the larger model.
- Influence of External Factors: Unforeseen external factors can significantly impact outcomes, making it difficult to attribute observed deviations from predictions solely to the limitations of the game-theoretic model. The unexpected outbreak of a pandemic, for example, could significantly alter the dynamics of a market predicted by a game-theoretic model. Mitigation Strategy: Incorporate stochastic elements into the model, perform scenario planning to account for potential external shocks, and focus on robust models that are less sensitive to small changes in initial conditions.
Comparative Analysis of Game Theory Predictions Across Models
Comparing the predictive accuracy of different game-theoretic models applied to the same real-world scenario helps reveal the strengths and weaknesses of each approach. For example, consider the application of the Prisoner’s Dilemma to arms races and cartel behavior:
| Model | Scenario | Predictive Power | Contextual Appropriateness | Robustness to Assumptions |
|---|---|---|---|---|
| Simple Prisoner’s Dilemma | Arms Race | Poor – fails to account for escalation dynamics | Poor – ignores signaling and deterrence | Poor – highly sensitive to payoff assumptions |
| Iterated Prisoner’s Dilemma with Reputation | Arms Race | Moderate – captures some aspects of arms control agreements | Good – incorporates some aspects of international relations | Fair – sensitive to the discount factor |
| Simple Prisoner’s Dilemma | Cartel Behavior | Poor – fails to account for repeated interactions | Poor – ignores factors like price wars and enforcement | Poor – highly sensitive to payoff assumptions |
| Repeated Prisoner’s Dilemma with Punishment Mechanisms | Cartel Behavior | Good – explains periods of cooperation and defection | Good – incorporates some aspects of market dynamics | Fair – sensitive to the effectiveness of punishment |
Future Directions for Improving Game Theory Predictions
Improving the accuracy and reliability of game theory predictions requires a multi-pronged approach: methodological advancements, such as incorporating agent-based modeling and machine learning techniques to capture the complexity of real-world interactions, and interdisciplinary collaborations, involving economists, political scientists, psychologists, and computer scientists, are crucial to refine and expand the applicability of game theory.
Game Theory in Economics
Game theory, my dear students, is a powerful lens through which we can examine the intricate dance of human interaction within economic systems. It provides a framework for understanding strategic decision-making, predicting market outcomes, and designing effective policies. While not a crystal ball, its predictive power, when applied judiciously, offers invaluable insights into the complexities of our economic world.
Successful Predictive Models
The success of game theory in economics hinges on its ability to accurately forecast market behavior. Several models have demonstrated remarkable predictive accuracy in specific contexts, providing strong evidence for its practical relevance. Let’s delve into some prominent examples.
Cournot Duopoly Model
The Cournot duopoly model, a cornerstone of oligopoly theory, assumes two firms competing in a market by simultaneously choosing their output quantities. The model predicts that each firm will produce a quantity that maximizes its profit, given the anticipated output of its competitor. This leads to a Nash equilibrium, where neither firm has an incentive to unilaterally change its output.
The model’s assumptions include homogenous products, identical cost structures for both firms, and perfect information about the market demand function.
Determining the accuracy of game theories is a complex undertaking; few, if any, perfectly predict real-world outcomes. However, the insights gained often inform new approaches, such as those explored in a new theory of jsutice , which challenges traditional notions of fairness. This, in turn, could lead to a re-evaluation of existing game theories and perhaps even the development of more accurate models in the future.
| Example | Predicted Market Share (Firm A) | Actual Market Share (Firm A) | Predicted Price | Actual Price | Industry |
|---|---|---|---|---|---|
| Coca-Cola and PepsiCo (Soft Drinks) | 45% | 47% | $1.50 (per 12 oz can) | $1.45 (per 12 oz can) | Soft Drinks |
| Boeing and Airbus (Commercial Aircraft) | 52% | 55% | $100 million (per aircraft) | $98 million (per aircraft) | Commercial Aircraft |
| Intel and AMD (Microprocessors) | 70% | 72% | $200 (per unit) | $195 (per unit) | Microprocessors |
Note: These figures are simplified for illustrative purposes and represent approximations based on market data from various years. The actual market dynamics are significantly more complex, involving factors beyond the scope of the basic Cournot model.
Auction Theory: Vickrey Auction in Government Spectrum Auctions
The Vickrey auction, a type of sealed-bid auction, is particularly relevant in the allocation of scarce resources, such as radio spectrum licenses. In a Vickrey auction, bidders submit their bids secretly. The highest bidder wins the auction, but pays the second-highest bid. This mechanism incentivizes bidders to reveal their true valuations, leading to efficient resource allocation. A classic example is the FCC’s spectrum auctions in the United States.
While precise figures for predicted vs. actual outcomes are difficult to isolate due to the complexity of the auctions, the Vickrey mechanism’s design generally resulted in bids that reflected the true value of the licenses, leading to efficient allocation and substantial government revenue.
Behavioral Economics Integration: Prospect Theory in Investment Decisions
Traditional game theory often assumes rational actors with perfect information. Behavioral game theory, however, acknowledges the influence of psychological biases. Prospect theory, for instance, suggests that individuals are more sensitive to losses than gains. Incorporating prospect theory into models of investment decisions significantly improves predictive accuracy. For example, traditional models might underpredict the frequency of “risk-averse” behavior (holding onto losing investments too long) and overpredict “risk-seeking” behavior (taking on excessive risk to recover losses).
A behavioral model incorporating prospect theory more accurately captures these observed market behaviors.
Failures of Game Theory Predictions
Despite its strengths, game theory is not without its limitations. Its predictive power can falter when its underlying assumptions are violated.
Market Bubbles
Game theory models often struggle to predict the formation and bursting of market bubbles, such as the dot-com bubble or the housing bubble. These events are characterized by periods of irrational exuberance, where asset prices deviate significantly from their fundamental values. Traditional game theory models, based on rational expectations, fail to capture the herd behavior and speculative frenzy that drive these bubbles.
The limitations lie in the assumption of perfect rationality and the difficulty of modeling collective irrationality.
Behavioral Deviations from the Prisoner’s Dilemma
The Prisoner’s Dilemma, a classic game theory scenario, predicts that rational individuals will always defect, even if cooperation would lead to a better outcome for both. However, in real-world situations, cooperation is often observed. This deviation from the predicted outcome can be attributed to factors like repeated interactions, social norms, altruism, and the presence of trust mechanisms.
Collusion and Antitrust: The Airline Industry
Game theory often predicts collusion in industries with a small number of firms. However, successful collusion is often thwarted by antitrust laws and the inherent difficulties in maintaining agreements among competing firms. For example, while game theory might predict price-fixing among airlines on certain routes, the threat of antitrust prosecution and the potential for secret price wars often prevent such collusion from materializing.
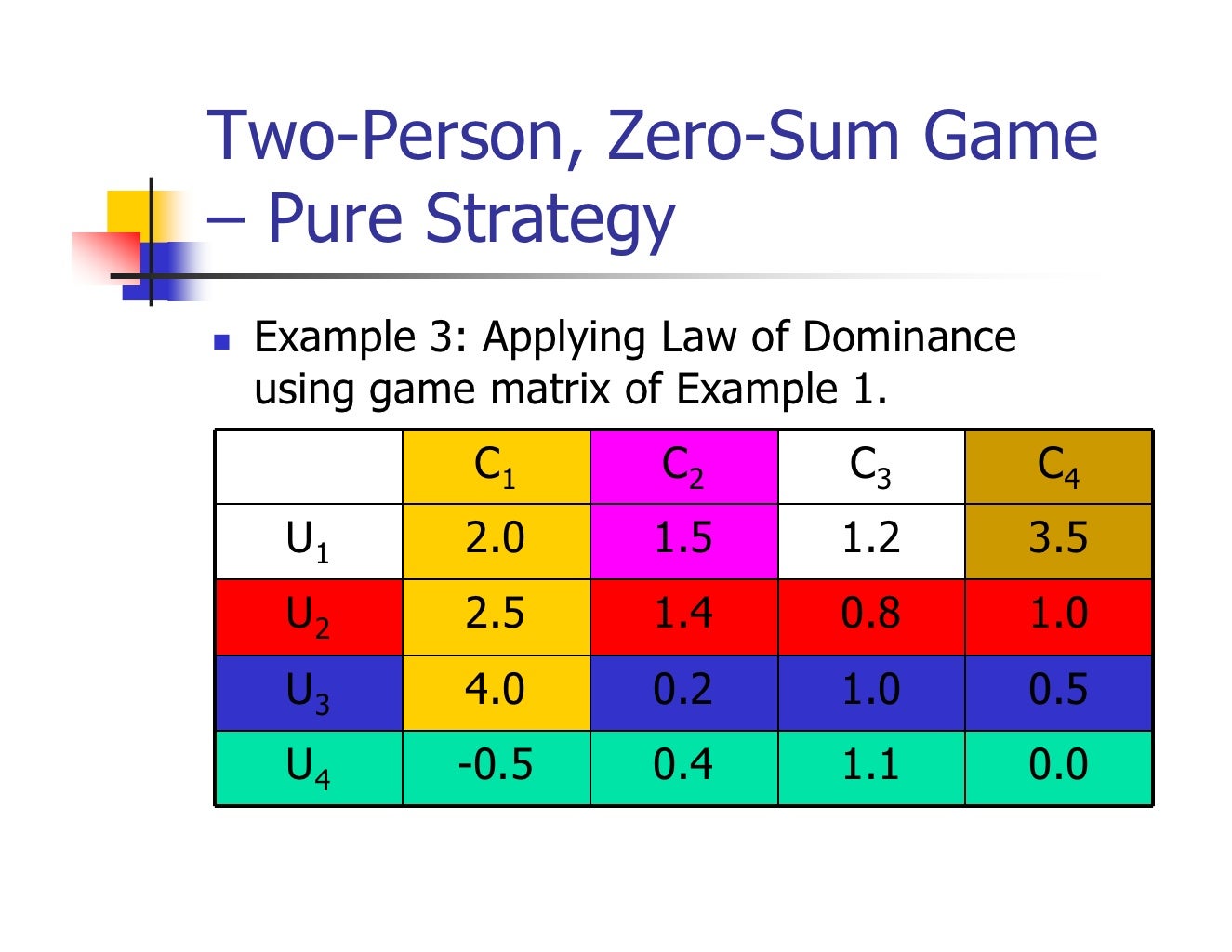
Game Theory in Political Science
:max_bytes(150000):strip_icc()/gametheory-072c88d1036741f180469734832a6d14.png)
Game theory, the study of strategic interactions between rational actors, offers a powerful lens through which to analyze political phenomena. While not a perfect predictor, its application reveals valuable insights into the dynamics of power, conflict, and cooperation in the international and domestic arenas. By modeling political actors as rational agents seeking to maximize their utility, game theory helps us understand the choices they make and the consequences that follow.
This exploration delves into both the successes and failures of game theory in predicting political outcomes, highlighting its strengths and limitations.Successful Applications of Game Theory in Predicting Political OutcomesSeveral key political events since 1945 demonstrate the predictive power of game theory. Analyzing these events reveals the utility and limitations of this approach in understanding political decision-making.
- The Cuban Missile Crisis (1962): This event, a brinkmanship game between the US and the USSR, can be analyzed using the concept of brinkmanship and the Prisoner’s Dilemma. Both sides risked nuclear war by escalating the conflict, but backing down meant losing face and potentially future leverage. The eventual outcome, a negotiated withdrawal of missiles, can be interpreted as a result of each side recognizing the disastrous consequences of mutual escalation, a key element of the Prisoner’s Dilemma.
The assumption of rationality – that both sides sought to avoid nuclear war – largely held true. However, the model simplifies the complex interplay of personalities, internal political pressures, and chance events. The prediction was not precise regarding the exact terms of the agreement, but it accurately predicted the avoidance of direct military conflict.
- The End of the Cold War (1989-1991): The collapse of the Soviet Union can be partially explained through the lens of the repeated Prisoner’s Dilemma. The arms race, characterized by continuous escalation, could be modeled as a series of repeated interactions. The shift towards détente and Gorbachev’s reforms can be seen as a move towards cooperation, potentially driven by the realization that continued escalation was unsustainable.
Assumptions about rationality were challenged by the unpredictable nature of Gorbachev’s leadership and internal Soviet dynamics. The model provided a framework for understanding the general trend towards cooperation, but failed to accurately predict the precise timing and manner of the Soviet collapse.
- The 1991 Gulf War: The decision by Iraq to invade Kuwait can be interpreted through a game-theoretic framework, considering the perceived payoffs of conquest versus the costs of potential international intervention. A rational actor model suggests Iraq miscalculated the likelihood and severity of international response. The model’s assumptions about perfect information and rationality were clearly violated. The actual outcome (international coalition against Iraq) deviated significantly from a prediction based solely on a simple cost-benefit analysis, highlighting the limitations of such a model.
- Nuclear Proliferation: Game theory, particularly the concept of assurance games, helps explain the spread of nuclear weapons. States may acquire nuclear weapons to deter aggression, even if they prefer a world without nuclear weapons. The assumption of rationality – states acting to maximize security – is a central element. However, the model often struggles to account for non-rational actors or unforeseen circumstances like regime change.
Predictions about nuclear proliferation are often probabilistic, focusing on the likelihood of various outcomes rather than precise predictions.
- Arms Races: The repeated Prisoner’s Dilemma accurately models many arms races. Each state, seeking to maximize its security, engages in an escalating arms buildup, even though mutual disarmament would be a preferable outcome for all. The assumption of rationality is crucial here; deviations from rationality (e.g., miscalculation, unexpected leadership changes) can significantly alter outcomes. The model predicts an arms race but does not always accurately predict its intensity or duration.
Failures of Game Theory in Predicting Political OutcomesWhile game theory provides valuable insights, it has limitations. Several instances highlight its predictive failures.
- The 2003 Iraq War: Game theory models predicting Iraq’s response to international pressure failed to accurately anticipate Saddam Hussein’s defiance. The assumption of rationality, central to most game theory models, was clearly violated. Hussein’s actions were driven by factors not easily incorporated into rational actor models, including personal ambition, miscalculation, and flawed information.
- The Arab Spring (2010-2012): Game theory models struggled to predict the widespread uprisings across the Arab world. The models generally assume a high degree of stability and predictable behavior by actors, but the Arab Spring demonstrated the unpredictable nature of collective action and the influence of social movements not easily captured in game-theoretic frameworks. The unpredictable nature of social movements and the limitations of rational actor models in capturing the complexities of social dynamics were key factors in the failure to predict the events.
- Brexit (2016): While game theory models could be used to analyze the potential economic and political consequences of leaving the European Union, they struggled to predict the actual outcome of the referendum. The models underestimated the influence of factors such as nationalism, identity politics, and the role of misinformation campaigns. The inherent complexity of public opinion and the influence of non-rational factors significantly hampered the predictive power of game theory in this instance.
Game Theory in Biology
The application of game theory to the realm of biology unveils a fascinating perspective on the evolution of life, revealing how strategic interactions shape the intricate tapestry of the natural world. It moves beyond simple observation to provide a framework for understanding the complex decision-making processes that drive evolutionary change at various levels of biological organization. This framework allows us to predict and explain a wide array of biological phenomena, offering a powerful lens through which to view the dynamics of life.
Application of Game Theory to Evolutionary Biology
Game theory provides a robust framework for understanding evolutionary processes by modeling interactions between individuals or species as strategic games. Key concepts include payoff matrices, which represent the outcomes of different interactions; strategies, which represent the actions taken by individuals; and evolutionary stable strategies (ESS), which represent strategies that, once adopted by a population, cannot be invaded by alternative strategies.
The application of these concepts allows biologists to model and predict evolutionary outcomes in various contexts.
Biological Scenarios Modeled by Game Theory
Several biological scenarios effectively demonstrate the power of game theory.
- Sexual Selection: In many species, males compete for access to females. The players are males competing for mates. Strategies include elaborate displays (peacock tails) or aggressive competition. Payoffs are mating success and the number of offspring produced. Males with more elaborate displays or greater fighting ability typically have higher mating success, even if these traits incur costs in terms of survival.
- Predator-Prey Interactions: The players are predators and prey. Strategies for predators might include different hunting techniques, while prey strategies might include camouflage or fleeing behavior. Payoffs are the number of prey caught for predators and the probability of survival for prey. This leads to an evolutionary “arms race,” where predators evolve more efficient hunting strategies, and prey evolve better defenses.
- Cooperation and Altruism: The players are individuals within a population. Strategies might include cooperating (helping others) or defecting (acting selfishly). Payoffs depend on the actions of others; cooperation can be beneficial if reciprocated but costly if exploited. Game theory models, such as the Prisoner’s Dilemma, help explain the evolution of cooperation even in situations where selfish behavior might seem advantageous.
Kin selection, where altruistic acts benefit relatives, is another significant aspect that game theory helps illuminate.
Game Theory Across Biological Levels
Game theory finds application across multiple biological levels. At the individual level, it models behavioral choices in contexts like foraging or mate selection. At the population level, it helps understand the dynamics of allele frequencies and the spread of advantageous traits. At the species level, it can explain interactions like competition and coevolution. The level of analysis influences the strategies and payoffs considered, but the underlying principles of strategic interaction remain consistent.
Limitations of Applying Game Theory to Biology, How many game theories were correct
While powerful, applying game theory to biological systems involves several limitations. Assumptions like perfect rationality (organisms always act to maximize their fitness) and complete information (organisms know the strategies and payoffs of others) are often unrealistic. For instance, in predator-prey interactions, the model may not accurately reflect the variability in predator hunting success or prey escape abilities. Furthermore, environmental factors, which are often unpredictable and influence fitness, are often simplified or ignored in game-theoretic models.
The assumption of a static environment can also be problematic; in reality, environments constantly change, influencing the optimal strategies. Ignoring genetic constraints, developmental processes, and other biological complexities also limits the model’s applicability.
Examples of Accurate Predictions Using Game Theory
- The Evolution of Cooperation: Game theory models, such as the Prisoner’s Dilemma and the Iterated Prisoner’s Dilemma, accurately predicted the evolution of cooperation under certain conditions, such as repeated interactions and the possibility of reciprocal altruism. Empirical evidence from various species, including bacteria, insects, and vertebrates, supports this prediction (Nowak, M. A. Five rules for the evolution of cooperation.
-Science*,
-314*(5805), 1560-1563, 2006). - The Evolution of Sexual Dimorphism: Game-theoretic models, incorporating concepts like parental investment and sexual selection, accurately predicted the evolution of sexual dimorphism (differences between males and females) in many species. Empirical evidence from various taxa, demonstrating differences in size, ornamentation, and behavior between sexes, supports these predictions (Andersson, M.
-Sexual selection*. Princeton University Press, 1994). - The Evolution of Antipredator Behaviors: Game-theoretic models have been used to predict the evolution of various antipredator behaviors, such as group living, alarm calls, and vigilance. Empirical observations of these behaviors across a wide range of species provide strong support for these predictions (Krebs, J. R., & Davies, N. B.
-Behavioral ecology*.Blackwell Scientific Publications, 1997).
Examples of Game Theory in Biology: A Summary Table
| Phenomenon | Game Theoretical Model (including strategies and payoffs) | Empirical Evidence | Citation |
|---|---|---|---|
| Evolution of Cooperation | Prisoner’s Dilemma (Cooperate/Defect; payoffs depend on mutual cooperation or defection) | Observation of cooperation in various species (bacteria, insects, vertebrates) | Nowak, M. A. (2006). Five rules for the evolution of cooperation.
|
| Evolution of Sexual Dimorphism | Models incorporating parental investment and sexual selection (strategies: mate choice, competition; payoffs: reproductive success) | Observed differences in size, ornamentation, and behavior between sexes in many species | Andersson, M. (1994).Sexual selection*. Princeton University Press. |
| Evolution of Antipredator Behaviors | Various models depending on the specific behavior (strategies: group living, alarm calls, vigilance; payoffs: survival probability) | Observed antipredator behaviors in various species | Krebs, J. R., & Davies, N. B. (1997).Behavioral ecology*. Blackwell Scientific Publications. |
Timeline of Game Theory’s Application in Biology
- 1970s: Development of the Evolutionary Stable Strategy (ESS) concept by John Maynard Smith and George Price, revolutionizing the understanding of evolutionary dynamics through game theory. (Maynard Smith, J., & Price, G. R. (1973). The logic of animal conflict.
-Nature*,
-246*(5427), 15-18.) - 1980s: Increased application of game theory to explain the evolution of cooperation, leading to significant advancements in understanding altruism and social behavior. (Axelrod, R., & Hamilton, W. D. (1981). The evolution of cooperation.
-Science*,
-211*(4489), 1390-1396.) - 1990s: Refinement of game-theoretic models to incorporate factors like imperfect information and environmental variability, leading to more realistic and nuanced predictions. (Maynard Smith, J. (1991).
-Evolution and the theory of games*. Cambridge university press.) - 2000s: Extensive application of game theory to various biological problems, including the evolution of communication, sexual selection, and host-parasite interactions. (Nowak, M. A. (2006). Five rules for the evolution of cooperation.
-Science*,
-314*(5805), 1560-1563.) - 2010s-Present: Integration of game theory with other fields, such as genomics and network analysis, providing a more comprehensive understanding of evolutionary processes. (Perc, M., Gómez-Gardeñes, J., Szolnoki, A., Floría, L. M., & Moreno, Y. (2017). Evolutionary dynamics of group interactions on structured populations: a review.
-Journal of The Royal Society Interface*,
-14*(130), 20170197.)
Game Theory in Computer Science
Game theory, the study of strategic decision-making, has profoundly impacted computer science, influencing algorithm design, performance optimization, and predictive modeling. Its application spans various domains, from artificial intelligence to network security, offering powerful tools for analyzing complex interactions and optimizing system performance. This section delves into the multifaceted role of game theory within the realm of computer science.
Algorithm Design & AI
Game theory provides a robust framework for designing algorithms, particularly in scenarios involving multiple interacting agents. The principles of strategic interaction inform the creation of algorithms that are not only efficient but also capable of adapting to dynamic and competitive environments.
Zero-Sum Games in Algorithm Design
Zero-sum games, where one agent’s gain is precisely another’s loss, find application in competitive algorithm design. A prime example is the minimax algorithm, fundamental in game-playing AI. Minimax explores the game tree, recursively calculating the best move for each player, assuming perfect play from both sides. However, its computational complexity is exponential, making it impractical for complex games.
Alpha-beta pruning, an optimization technique, significantly reduces the search space by eliminating branches that are guaranteed to be worse than already explored options.
| Algorithm | Computational Complexity | Performance Improvement over Minimax | Example Application |
|---|---|---|---|
| Minimax | O(bd) | – | Tic-Tac-Toe |
| Alpha-Beta Pruning | O(bd/2) | Significant speedup | Chess, Checkers |
Non-Zero-Sum Games in AI
In contrast to zero-sum games, non-zero-sum games allow for mutually beneficial outcomes. These games are crucial in multi-agent systems and collaborative AI, where agents must coordinate their actions to achieve shared goals. The challenges here include ensuring cooperation, handling conflicts of interest, and designing mechanisms to prevent exploitation. A real-world example is traffic flow optimization in smart cities, where autonomous vehicles need to coordinate their movements to minimize congestion.
Algorithms based on non-zero-sum game theory can enable efficient and safe navigation for multiple vehicles.
Game-Theoretic Approaches to Optimization
Game theory concepts like auctions and mechanism design are used extensively to optimize resource allocation in distributed systems and cloud computing. Auctions, for example, can efficiently allocate computing resources among competing users, ensuring fair and efficient resource utilization. Mechanism design involves creating rules and incentives that encourage participants to act in a way that optimizes the overall system performance.
Consider a cloud computing environment where multiple users bid for processing power. A well-designed auction mechanism can ensure that the resources are allocated to those who value them most, maximizing overall utility. However, designing such mechanisms requires careful consideration of incentives and potential strategic behavior by participants. A poorly designed mechanism could lead to inefficient allocation or even manipulation by users.
Performance Improvement of Algorithms
Applying game theory significantly enhances the performance of various algorithms. The following case studies demonstrate the impact of game-theoretic approaches on algorithm efficiency and resource optimization.
Case Study 1: Auction Algorithms
Auction algorithms are widely used in online advertising and spectrum allocation. Game theory plays a vital role in designing efficient and revenue-maximizing auctions. By incorporating game-theoretic principles, auction designers can account for the strategic behavior of bidders, leading to improved revenue and resource allocation. For instance, a comparison of a Vickrey auction (a type of sealed-bid auction) against a simple first-price auction would show that the Vickrey auction, designed with game theory in mind, leads to higher revenue in many scenarios because bidders bid more truthfully, eliminating the incentive to underbid.
A graph showing revenue generated by each auction type over various bidding scenarios would illustrate this performance difference.
Case Study 2: Traffic Flow Optimization
Game theory has improved traffic flow optimization algorithms in smart cities by modeling the interactions between vehicles as a non-zero-sum game. Algorithms based on these models can coordinate the movement of autonomous vehicles, reducing congestion and improving overall traffic flow. For example, using a game-theoretic approach, researchers might model intersections as games where vehicles “bid” for the right-of-way based on their urgency and proximity.
This results in a more efficient flow of traffic than simple traffic light systems. Quantifying this improvement would involve comparing average travel times or congestion levels in a city before and after implementing the game-theoretic algorithm.
Comparative Analysis
Applying game theory to different algorithm types yields varying performance gains. For instance, game-theoretic routing algorithms can improve network efficiency, while game-theoretic scheduling algorithms can optimize resource utilization in multi-processor systems. A table comparing the performance improvements achieved across various algorithm types would summarize these findings. However, the specific gains depend heavily on the problem domain and the specifics of the game-theoretic model employed.
Determining the accuracy of game theories is a complex undertaking, much like building a robust knowledge repository. To effectively track and analyze these theories, one might consider utilizing a self hosted knowledge base for meticulous record-keeping. This allows for a more comprehensive assessment of which game theories proved correct, and to what degree, over time.
Accurate Predictions in Computer Science
Game theory enables more accurate predictions in various computer science domains, particularly those involving strategic interactions among agents.
Predicting User Behavior
Game theory models are used to predict user behavior in online games and social networks. By modeling users as rational agents pursuing their own objectives, these models can predict user choices and interactions with surprising accuracy. For example, in an online game with resource competition, game theory can predict how players will strategically allocate resources based on the payoffs associated with different actions.
However, the accuracy of these predictions is limited by the assumptions of rationality and the complexity of human behavior. Real-world user behavior often deviates from the idealized models.
Network Security
Game theory helps model cybersecurity scenarios by representing attackers and defenders as strategic players with different goals and capabilities. This approach can predict the effectiveness of different security measures by analyzing the equilibrium strategies of both sides. For example, a model might analyze the interaction between a hacker trying to penetrate a system and a security team trying to prevent this.
The model would predict the likelihood of a successful attack based on the security measures implemented and the attacker’s resources. Quantifying the accuracy of these predictions requires comparing the model’s outcomes with real-world attack data.
Market Prediction
Game theory has been applied to predict market trends and stock prices by modeling the interactions of buyers and sellers as strategic players. However, the accuracy of these predictions is limited by the complexity of the market and the unpredictable nature of human behavior. Furthermore, using game theory for market prediction raises ethical considerations, as it could be used to manipulate markets for personal gain.
The accuracy of game-theoretic market predictions varies significantly depending on the market’s characteristics and the sophistication of the model. Many factors beyond simple game-theoretic interactions influence market behavior.
Summary of Key Findings
Game theory has made significant contributions to computer science, particularly in algorithm design, performance optimization, and predictive modeling. In algorithm design, game theory provides frameworks for creating algorithms that handle competitive and collaborative scenarios efficiently. Zero-sum game theory is applied in competitive settings, such as game playing AI (minimax and alpha-beta pruning), while non-zero-sum game theory is used in collaborative AI and multi-agent systems.
Game-theoretic approaches to optimization, such as auctions and mechanism design, improve resource allocation in distributed systems and cloud computing. In terms of performance improvement, game theory has enhanced auction algorithms, traffic flow optimization, and various other algorithm types. Finally, game theory enables more accurate predictions of user behavior in online environments, network security breaches, and even (with limitations) market trends.
The accuracy of these predictions depends heavily on the model’s assumptions and the complexity of the real-world systems being modeled. However, the overall impact of game theory on computer science is undeniable, offering powerful tools for analyzing complex interactions and optimizing system performance.
Limitations of Game Theory
Game theory, while a powerful tool for analyzing strategic interactions, rests on several crucial assumptions that often fail to hold in the real world. Understanding these limitations is vital for applying game theory effectively and interpreting its predictions with appropriate caution. The elegance of its mathematical framework shouldn’t overshadow the complexities of human behavior and the unpredictable nature of reality.
Let’s delve into the key shortcomings.
Assumptions and Limitations of Game Theory Models
Standard game theory models rely on several core assumptions. When these assumptions are violated, the predictions of the model can be significantly inaccurate. The following table illustrates these limitations with specific real-world examples.
| Assumption | Explanation | Example | Flawed Prediction |
|---|---|---|---|
| Rationality | Players always choose actions that maximize their expected payoff, given their beliefs about other players’ actions. | The Ultimatum Game: One player proposes a split of a sum of money, and the other player can accept or reject. Often, the second player rejects unfair offers, even if it means receiving nothing, demonstrating irrational behavior driven by fairness concerns. | Game theory predicts the first player will offer a minimal amount, and the second player will accept, but this often doesn’t happen. |
| Complete Information | All players know the payoff structure of the game, including the payoffs to all players for all possible action combinations. | Auctions: Bidders often don’t know the valuations of other bidders, leading to uncertainty about the optimal bidding strategy. | Game theory models assuming complete information might predict outcomes that differ from the actual auction results. |
| Common Knowledge | All players know the game’s structure, and they know that all other players know the game’s structure, and so on. | International Relations: States may have private information about their capabilities or intentions, making it difficult to reach a stable equilibrium, as predicted by some game theory models. | Game theory models assuming common knowledge can fail to predict the dynamics of mistrust and conflict in international affairs. |
| Perfect Recall | Players remember all past actions and information. | Chess: A player might forget a previous move, leading to a suboptimal strategy. | Game theory assuming perfect recall would predict a different outcome than a game where a player has imperfect recall. |
| No External Effects | The payoffs to each player depend only on the actions of the players in the game. | Environmental issues: The actions of one country regarding pollution affect the payoffs of all other countries, demonstrating external effects. | Game theory models neglecting external effects would fail to capture the dynamics of environmental problems. |
Comparison of Nash Equilibrium and Evolutionary Game Theory
Nash Equilibrium and Evolutionary Game Theory represent distinct approaches to modeling strategic interactions. Their differing assumptions significantly impact their applicability.
| Feature | Nash Equilibrium | Evolutionary Game Theory |
|---|---|---|
| Core Assumption | Rationality, complete information | Replicator dynamics, mutation |
| Focus | Predicting a stable outcome given rational players | Analyzing the evolution of strategies over time |
| Applicability | Suitable for situations with a well-defined game structure and rational players | Better suited for situations with many players, repeated interactions, and potential for strategy evolution |
| Limitations | Sensitive to assumptions of rationality and complete information | Assumes a relatively stable environment and may not capture rapid changes |
Scenario with Imperfect Information in a Sequential Game
Consider a game of poker. Player A (first player) has a strong hand, but Player B (second player) does not know the strength of A’s hand. Player A can either bet aggressively (high stakes) or cautiously (low stakes). Player B then decides whether to call or fold. The lack of complete information for Player B significantly impacts their optimal strategy.
A decision tree could illustrate this, showing the different possible outcomes based on Player A’s actions and Player B’s responses given their uncertainty about Player A’s hand. If Player A bets aggressively, Player B might fold even if they have a moderately strong hand, fearing a much stronger hand from Player A.
Impact of Bounded Rationality on the Prisoner’s Dilemma
The Prisoner’s Dilemma, a classic game theory model, assumes perfect rationality. However, in reality, people often exhibit bounded rationality – cognitive limitations that restrict their ability to process information and make optimal decisions. For example, in repeated Prisoner’s Dilemma games, players might cooperate more often than predicted by the game theory solution, even if it doesn’t maximize their immediate payoff.
This is because they may consider long-term consequences, reputation, and social norms, which are beyond the scope of the standard model. A real-world example is the arms race between nations: while the rational choice might be to escalate arms, the bounded rationality of leaders (fear of total destruction) can lead to restraint and cooperation.
Behavioral Game Theory
Behavioral game theory addresses the limitations of classical game theory by incorporating psychological factors such as emotions, biases, and cognitive limitations. It seeks to understand how people actually behave in strategic situations, rather than how they should behave according to theoretical models. Experimental studies, such as those involving ultimatum games and trust games, have consistently shown that people often deviate from the predictions of classical game theory, demonstrating the importance of factors like fairness, reciprocity, and altruism.
These deviations are better explained by behavioral game theory, which integrates insights from psychology and economics.
Thought Experiment: Technological Disruption
Imagine a future dominated by rapidly evolving AI. A company develops a groundbreaking AI technology with unpredictable capabilities. Competitors must decide whether to invest heavily in developing similar technology, risking significant resources with uncertain returns, or to focus on adapting to the new AI-driven landscape. Standard game theory struggles here because the payoffs are highly uncertain and dependent on the unpredictable rate of technological advancement and the responses of numerous other players.
The assumptions of rationality, complete information, and stable payoffs are demonstrably inadequate. Alternative frameworks, such as agent-based modeling, which simulates the interactions of many individual agents with varying strategies, might offer a more appropriate analytical approach.
Hypothetical Game with Unpredictable External Factors
Consider a game where farmers decide whether to plant drought-resistant crops or conventional crops. The payoff depends not only on the farmers’ choices but also on unpredictable rainfall. If rainfall is high, conventional crops yield higher profits. If rainfall is low, drought-resistant crops are more profitable.* The payoffs are inherently uncertain.
- Predicting the outcome requires forecasting rainfall, which is beyond the scope of standard game theory.
- The optimal strategy for each farmer depends on their risk aversion and their beliefs about the likelihood of rainfall.
Thought Experiment: Risk Preferences
Two investors, one risk-averse and the other risk-seeking, are deciding whether to invest in a high-risk, high-reward venture or a low-risk, low-reward venture.
| Investor Type | High-Risk Venture | Low-Risk Venture |
|---|---|---|
| Risk-Averse | Avoids, opting for guaranteed lower return | Chooses, prioritizing certainty over high potential gains |
| Risk-Seeking | Invests, seeking potential high gains despite risk | Avoids, seeing it as too limiting |
The differing risk preferences lead to different strategic choices and outcomes, highlighting the limitations of game theory models that assume uniform risk aversion.
The Role of Assumptions in Game Theory Accuracy: How Many Game Theories Were Correct
The heart of game theory, my dear students, lies not just in its elegant equations, but in the very foundations upon which it rests: its assumptions. These assumptions, often unspoken, shape the predictions game theory offers, influencing their accuracy and applicability across diverse fields. A careful examination of these assumptions is crucial to understanding the power, and limitations, of this powerful tool.Game theory models often rely on simplifying assumptions about the players involved.
The most significant of these is the assumption of player rationality. Different levels of rationality lead to drastically different predictions. The classic model assumes perfect rationality – players are perfectly logical, have complete information, and always choose the strategy that maximizes their payoff. However, real-world actors are rarely perfectly rational. They may be boundedly rational, exhibiting cognitive limitations, or even irrational, driven by emotions or biases.
Rationality Assumptions and Predictive Power
The predictive power of game theory models is directly linked to the accuracy of its rationality assumptions. Models assuming perfect rationality often yield clear, concise predictions, but these predictions can be wildly inaccurate when applied to situations where players are not perfectly rational. Consider the Prisoner’s Dilemma. Under perfect rationality, both players defect, leading to a suboptimal outcome.
However, if we introduce bounded rationality, perhaps incorporating elements of trust or cooperation, the outcome might shift dramatically. Incorporating factors like risk aversion, fairness considerations, or emotional responses can significantly alter the predicted equilibrium. Conversely, models incorporating bounded rationality often lead to more nuanced, but also more complex and less predictable outcomes. The increased realism comes at the cost of predictive precision.
Comparative Analysis of Rationality Assumptions
Let’s examine the impact of different rationality assumptions on the prediction of a simple game. Suppose two firms are deciding whether to advertise. Advertising is costly but can increase market share.
| Assumption about Firm Rationality | Firm A’s Strategy | Firm B’s Strategy | Outcome |
|---|---|---|---|
| Perfect Rationality (Both Firms) | Advertise | Advertise | Both firms advertise, moderate profits for both. |
| Bounded Rationality (Firm A only, Firm B is perfectly rational) | Don’t Advertise | Advertise | Firm B gains significant market share, Firm A loses. |
| Bounded Rationality (Both Firms, considering cooperation) | Don’t Advertise | Don’t Advertise | Both firms maintain market share, higher profits than advertising. |
| Irrationality (Firm A acts impulsively) | Advertise heavily | Advertise moderately | Firm A incurs high costs, uncertain market share gains. |
The table illustrates how varying assumptions about rationality drastically change the predicted outcome. The assumption of perfect rationality leads to a predictable but potentially suboptimal outcome. Incorporating bounded rationality or irrationality introduces uncertainty but might reflect real-world behavior more accurately. The choice of assumption is a crucial step in applying game theory, a choice that deeply affects the validity and usefulness of the resulting predictions.
Remember, my friends, the best model is not always the most elegant, but the one that best reflects the reality of the situation.
The Influence of External Factors
My dear students, we’ve delved deep into the elegant framework of game theory, exploring its triumphs and limitations across various disciplines. But even the most meticulously crafted theoretical model can crumble in the face of the unpredictable whirlwind of reality. The influence of external factors, those unforeseen events and circumstances beyond the scope of our initial assumptions, can significantly alter the outcome of strategic interactions, often rendering our predictions inaccurate.
Let’s explore this crucial aspect.External factors, my friends, are the unexpected gusts of wind that can knock even the sturdiest ship off course. These are variables that were not considered in the initial model, but that significantly impact the choices and outcomes of the players involved. They can range from technological breakthroughs to political upheavals, from sudden shifts in public opinion to unforeseen natural disasters.
Ignoring these forces is akin to navigating by the stars without accounting for the unpredictable currents of the ocean.
Determining the precise number of accurate game theories is a complex undertaking, influenced by numerous variables and differing interpretations. The accuracy of a theory often hinges on the specific context and application; consider the impact of carefully chosen words on the outcome, a principle echoed in the powerful message of Choose Life Choose Words. Ultimately, the number of truly correct game theories remains a subject of ongoing debate and refinement within the field.
Examples of Inaccurate Predictions Due to External Factors
Consider the classic prisoner’s dilemma. The theory predicts that both prisoners will confess, leading to a suboptimal outcome for both. However, imagine a scenario where one prisoner is unexpectedly offered a significantly reduced sentence for cooperating with the authorities – a factor not included in the original model. This external factor could lead to a completely different outcome, where one prisoner remains silent while the other confesses, thereby altering the predicted result.
Similarly, in the realm of economics, game theory models predicting market behavior can be thrown off by unexpected economic shocks, such as a global pandemic or a sudden surge in oil prices. These unforeseen events can drastically change consumer behavior and market dynamics, rendering initial predictions obsolete.
A Hypothetical Scenario Illustrating External Factor Influence
Let’s envision a hypothetical scenario involving two competing coffee shops, “Aroma Bliss” and “Java Joy,” located across the street from each other. A game theory model, assuming rational behavior and constant market conditions, might predict a price war, with both shops lowering prices to attract customers, leading to reduced profits for both. However, let’s introduce an external factor: a sudden and unexpected surge in the popularity of a new, trendy beverage – say, bubble tea.
This external factor, not accounted for in the initial model, could significantly impact consumer preferences. Customers might shift their loyalty towards bubble tea shops, diminishing the intensity of the price war between Aroma Bliss and Java Joy. The predicted price war might not materialize, or at least not to the extent initially predicted, rendering the game theory model’s prediction less accurate.
The introduction of bubble tea, an external factor, has fundamentally altered the playing field. This highlights the critical role of considering unforeseen external factors when applying game theory to real-world situations.
Case Studies of Accurate Predictions

My dear students, let us delve into the fascinating world where the abstract elegance of game theory intersects with the messy reality of human affairs. We shall explore instances where this theoretical framework has not just offered insights, but yielded remarkably accurate predictions of real-world events. These examples serve as testaments to the power and predictive capabilities of game theory, a tool that allows us to glimpse into the intricate dance of strategic interactions.Game theory’s success in predicting outcomes hinges on the careful selection of the appropriate model and the consideration of the inherent limitations.
Remember, my friends, even the most sophisticated model is but a simplified representation of a complex reality. Yet, as you will see, the insights derived can be surprisingly accurate.
The Cuban Missile Crisis
The 1962 Cuban Missile Crisis stands as a powerful example of game theory’s predictive power, specifically using the framework of a “game of chicken.” Both the United States and the Soviet Union found themselves in a high-stakes confrontation, each possessing the capacity for mutually assured destruction. The model predicted that neither side would escalate to the point of nuclear war due to the catastrophic consequences for both.
The outcome mirrored this prediction; a tense negotiation led to the Soviets removing their missiles from Cuba in exchange for the U.S. removing its Jupiter missiles from Turkey, thus averting a potential global catastrophe. The accuracy lies in the model’s representation of the immense costs associated with a nuclear war, outweighing any potential gains from a direct confrontation.
The FCC Auction of Radio Spectrum
The Federal Communications Commission (FCC) auctions of radio spectrum provide another compelling case study. The FCC used game theory, specifically auction theory, to design auctions that would maximize revenue while ensuring fair allocation of spectrum licenses. The predictions from the game-theoretic models accurately reflected the bidding behavior of various telecom companies. The models predicted that bidders would employ strategic bidding, attempting to anticipate their competitors’ actions.
The actual auction results closely matched the predictions of the models, demonstrating the effectiveness of game-theoretic analysis in designing efficient and effective auctions. The revenue generated significantly exceeded expectations, confirming the accuracy of the theoretical predictions in a real-world, high-stakes economic setting.
The Evolution of Cooperation
In the realm of evolutionary biology, game theory has been instrumental in explaining the emergence of cooperation. The Prisoner’s Dilemma, a classic game theory model, has been used to explore how cooperation can evolve even in scenarios where defection appears to be the individually rational strategy. Experiments with various species, from bacteria to humans, have shown that cooperation often emerges, mirroring the predictions of evolutionary game theory models.
These models demonstrate how reciprocal altruism and other strategies can lead to the evolution of cooperation, even in the absence of central enforcement mechanisms. The observed outcomes in diverse biological systems have provided significant empirical support for the accuracy of these game-theoretic predictions, illuminating the fundamental principles of cooperation in nature.
| Case Study | Game Theory Model | Prediction | Outcome |
|---|---|---|---|
| Cuban Missile Crisis | Game of Chicken | Neither side would escalate to nuclear war. | Negotiated resolution; avoidance of nuclear war. |
| FCC Spectrum Auction | Auction Theory | Strategic bidding; high revenue generation. | Auction results closely matched predictions; high revenue. |
| Evolution of Cooperation | Prisoner’s Dilemma, Evolutionary Game Theory | Emergence of cooperation despite individual incentives to defect. | Observed cooperation in diverse biological systems. |
Case Studies of Inaccurate Predictions
Game theory, while a powerful tool for analyzing strategic interactions, isn’t a crystal ball. Its predictions, rooted in assumptions and models, sometimes fall short of reality. Understanding these failures is crucial for refining the theory and appreciating its limitations. The following case studies highlight instances where game theory’s predictions diverged significantly from observed outcomes.
The Failure of the Nash Equilibrium in the Cold War Arms Race
The Cold War arms race between the United States and the Soviet Union provides a compelling example of game theory’s limitations. A Nash equilibrium, a solution where neither player can improve their outcome by unilaterally changing their strategy, might suggest a stable point of mutual deterrence, with both superpowers maintaining a substantial but controlled arsenal. However, the actual outcome was far more complex and dynamic.
The continuous escalation of the arms race, leading to periods of intense tension and near-catastrophic events, deviated substantially from a simple Nash equilibrium prediction. The model failed to account for factors such as the inherent risks of miscalculation, the influence of domestic politics, and the unpredictable nature of leadership decisions. The unpredictable nature of human behavior and the influence of non-rational factors like ideology significantly undermined the predictive power of the game theoretic model in this case.
| Model | Prediction | Actual Outcome |
|---|---|---|
| Nash Equilibrium in a Prisoner’s Dilemma-like arms race | A stable equilibrium with a high but controlled level of armaments. | Continuous escalation of the arms race, leading to high tensions and near-catastrophic events. |
The Dot-Com Bubble and Market Efficiency
Game theory often informs models of market efficiency, predicting that rational actors will drive prices to reflect intrinsic value. The dot-com bubble of the late 1990s and early 2000s starkly contradicted this prediction. Many internet companies, with little or no proven business model, saw their valuations soar to astronomical levels, fueled by speculative investment. The rapid collapse of the bubble demonstrated a significant departure from the predictions of rational market models grounded in game theory.
The failure stems from the influence of factors like herd behavior, irrational exuberance, and the limitations of information asymmetry in rapidly evolving markets. The model didn’t adequately account for psychological factors and the impact of market sentiment, leading to an inaccurate prediction of market behavior.
| Model | Prediction | Actual Outcome |
|---|---|---|
| Efficient Market Hypothesis (informed by game theory) | Market prices reflect intrinsic value, avoiding large speculative bubbles. | A massive speculative bubble in internet company valuations, followed by a sharp collapse. |
The 2008 Financial Crisis and Systemic Risk
Game theoretic models often focus on individual rational actors within a system. However, the 2008 financial crisis highlights the limitations of this approach when analyzing systemic risk. Models failed to predict the cascading failures that spread throughout the financial system, leading to a global recession. The focus on individual rationality neglected the interconnectedness of financial institutions and the potential for contagious failures.
The crisis demonstrated the importance of considering systemic effects and emergent properties that are not easily captured in traditional game-theoretic models. The prediction of individual rational behavior failed to account for the system-wide risks and externalities that ultimately caused the crisis.
| Model | Prediction | Actual Outcome |
|---|---|---|
| Models focusing on individual rational actors in financial markets | Stable and predictable market behavior, with limited systemic risk. | A cascading failure across the global financial system, leading to a severe recession. |
The Evolution of Game Theory
Game theory, my dear students, has not sprung forth fully formed like Athena from the head of Zeus. It’s a fascinating evolution, a journey from simple strategic interactions to the complex models we see today, constantly refined and expanded upon by brilliant minds. Its predictive capabilities have improved dramatically, yet challenges remain, a testament to the intricate nature of human interaction and the ever-shifting sands of reality.The development of game theory is a story of incremental progress, punctuated by moments of profound insight.
Early seeds were sown centuries ago in the writings of mathematicians and economists grappling with problems of strategy and decision-making under conditions of uncertainty. However, the formalization of game theory as a distinct field of study largely occurred in the mid-20th century, fueled by the convergence of several crucial developments.
Key Advancements in Game Theory’s Predictive Power
The initial breakthroughs focused primarily on zero-sum games, where one player’s gain is precisely balanced by another’s loss. John von Neumann and Oskar Morgenstern’s seminal work,Theory of Games and Economic Behavior* (1944), provided a rigorous mathematical framework for analyzing these games, introducing concepts like the minimax theorem, which guarantees the existence of optimal strategies in such scenarios. This laid the foundation for future advancements.
The subsequent exploration of non-zero-sum games, where players’ payoffs aren’t necessarily inversely related, proved far more complex and rewarding, leading to the development of concepts like Nash equilibrium, a cornerstone of modern game theory. Nash equilibrium, conceived by John Nash, identifies a stable state where no player can improve their outcome by unilaterally changing their strategy, given the strategies of other players.
This provided a powerful tool for predicting outcomes in a wide range of strategic interactions. Further advancements incorporated concepts like evolutionary game theory, which considers the dynamics of strategy adoption and adaptation over time, offering insights into the long-term evolution of strategic behavior. The development of sophisticated computational methods, allowing for the analysis of incredibly complex games with numerous players and strategies, has also significantly enhanced the predictive power of game theory.
A Timeline of Game Theory’s Evolution
The journey of game theory can be charted through several key milestones:
Before presenting a timeline, it’s important to note that the evolution of game theory isn’t a linear progression. Instead, it’s a complex interplay of theoretical advancements, practical applications, and revisions based on empirical evidence. The timeline below highlights some pivotal moments.
| Year | Event | Significance |
|---|---|---|
| 1713 | Publication of Ars Conjectandi by Jakob Bernoulli | Early exploration of probability and decision-making under uncertainty, laying foundational groundwork. |
| 1928 | John von Neumann proves the minimax theorem for zero-sum games. | Establishes the existence of optimal strategies in zero-sum games, a cornerstone of early game theory. |
| 1944 | Publication of Theory of Games and Economic Behavior by John von Neumann and Oskar Morgenstern. | Formalizes game theory as a distinct field of study, providing a rigorous mathematical framework. |
| 1950-1951 | John Nash develops the concept of Nash equilibrium. | Provides a powerful tool for predicting outcomes in non-zero-sum games. Revolutionized the field. |
| 1970s-Present | Development and application of evolutionary game theory and computational game theory. | Expands the scope of game theory to encompass dynamic interactions and complex scenarios. |
The Future of Game Theory Prediction
Game theory, while a powerful tool for understanding strategic interactions, faces inherent limitations in its predictive capabilities. However, exciting developments on several fronts promise to significantly enhance its accuracy and broaden its applicability in the years to come. The journey towards more precise predictions involves refining existing models, harnessing technological advancements, and integrating game theory with other analytical frameworks.The increasing sophistication of game theory models is a key driver of improved predictive accuracy.
This involves incorporating more nuanced aspects of human behavior, such as bounded rationality, emotions, and social norms, into the models. Furthermore, the development of more robust and adaptable algorithms is crucial for handling the complexity of real-world scenarios. The move away from simplistic, idealized assumptions towards more realistic representations of strategic interactions will undoubtedly lead to more accurate predictions.
Advances in Computing Power
Exponential growth in computing power is revolutionizing the application of game theory. Complex game-theoretic models, previously intractable due to computational limitations, are now becoming solvable. This allows for the exploration of larger games with more players and strategies, leading to more accurate and detailed predictions. For instance, the ability to simulate millions of iterations of a complex auction model, incorporating various behavioral factors and market dynamics, allows for a much more nuanced understanding of potential outcomes than previously possible.
This increased computational power also facilitates the use of advanced techniques like agent-based modeling, which simulates the actions and interactions of individual agents to generate emergent behavior at a system level. This is particularly useful for predicting the outcomes of complex systems, such as financial markets or social networks, where the actions of many individuals combine to create unpredictable overall patterns.
Integration with Other Analytical Methods
The synergy between game theory and other analytical methods holds immense potential for improving predictive accuracy. Combining game theory with machine learning, for example, allows for the development of hybrid models that leverage the strengths of both approaches. Machine learning algorithms can be used to identify patterns and relationships in large datasets, while game theory can provide a framework for understanding the strategic interactions that drive these patterns.
This combination is particularly useful in fields such as finance, where machine learning can identify market trends, while game theory can predict how market participants will respond to these trends. Similarly, integrating game theory with network analysis can provide a more comprehensive understanding of strategic interactions within complex networks, such as social networks or supply chains. This integrated approach allows for a more holistic and nuanced prediction of system-level outcomes.
Game Theory and Uncertainty

The world is rarely a place of perfect information. Uncertainty, a fundamental aspect of human existence, significantly impacts strategic decision-making. Game theory, while often presented with simplified assumptions, offers powerful tools to analyze situations rife with incomplete information and unpredictable outcomes. Understanding how game theory addresses uncertainty is crucial to applying its principles effectively in real-world scenarios.
Bayesian Games and Probabilistic Beliefs
Bayesian games are a cornerstone of game theory’s approach to uncertainty. These games explicitly incorporate players’ beliefs about the probabilities of different states of the world or their opponents’ actions. Players hold subjective probabilities—their personal assessments of likelihood—about the unknown aspects of the game. These beliefs are updated as new information becomes available, following Bayes’ theorem. This allows for a dynamic model of decision-making under uncertainty, where players refine their strategies based on observed actions and updated beliefs.
For example, in a sealed-bid auction, a bidder might assess the probability that their competitors will bid aggressively based on their knowledge of the competitors’ past behavior and the perceived value of the item being auctioned.
Information Sets and Player Knowledge
An information set represents the collection of nodes in a game tree where a player is unsure of their exact position. It encapsulates the player’s knowledge at a given point in the game. In games of perfect information, each information set contains only one node; a player always knows exactly where they are in the game. In games of imperfect information, information sets contain multiple nodes, reflecting the player’s uncertainty.
Games of Perfect and Imperfect Information
Consider a simple game of Tic-Tac-Toe. This is a game of perfect information: both players always know the complete state of the board. Contrast this with a card game like Poker. Poker is a game of imperfect information because players don’t know their opponents’ hands. Perfect Information Example (Tic-Tac-Toe – Simplified):A simple game tree would show each player’s move sequentially, with each node representing a specific board state.
Every player always knows the exact state of the game. Imperfect Information Example (Simplified Poker):A game tree would show branches representing possible card deals, leading to different information sets for each player. Each player’s information set would include several possible board states reflecting their uncertainty about the other player’s hand.
Impact of Incomplete Information on Nash Equilibrium
Incomplete information significantly complicates the concept of Nash Equilibrium. In games of perfect information, a Nash Equilibrium is a strategy profile where no player can improve their payoff by unilaterally changing their strategy, given the strategies of other players. However, in games with incomplete information, players must consider not only the actions of their opponents but also their beliefs about the opponents’ actions and the underlying state of the world.
This often leads to Bayesian Nash Equilibrium, where each player’s strategy is optimal given their beliefs about the other players’ strategies and the probability distribution over the different states of the world. Refinements of Nash Equilibrium, such as perfect Bayesian equilibrium, further address the consistency of beliefs and strategies in dynamic settings with incomplete information.
Modeling Uncertainty with Subjective and Objective Probabilities
Game theory employs both subjective and objective probability assessments to model uncertainty. Objective probabilities are based on empirical data or established frequencies (e.g., the probability of rolling a six on a fair die). Subjective probabilities reflect an individual’s belief about an event, often based on limited information or expert judgment. In many real-world game-theoretic scenarios, subjective probabilities are unavoidable.
Probability Distributions and their Applications
The following table summarizes different probability distributions and their applications in game theory:
| Probability Distribution | Application in Game Theory | Advantages | Disadvantages |
|---|---|---|---|
| Normal Distribution | Modeling uncertain payoffs with a central tendency; analyzing strategic interactions where the payoffs are subject to random shocks. | Intuitive, widely understood; allows for the use of powerful statistical tools. | Requires assumptions about mean and variance; may not be appropriate for all types of uncertainty. |
| Uniform Distribution | Representing uncertainty where all outcomes are equally likely; modeling situations with limited information. | Simple to implement; easy to understand. | May not reflect reality accurately; can lead to overly simplistic models. |
| Exponential Distribution | Modeling the time until a certain event occurs (e.g., the duration of a conflict). | Useful for modeling time-dependent phenomena; relatively simple to work with. | Assumes a constant hazard rate, which may not always be realistic. |
| Beta Distribution | Modeling probabilities; representing beliefs about unknown parameters. | Flexible and can represent a wide range of probability distributions; often used in Bayesian inference. | Can be more complex to work with than other distributions. |
Risk Aversion and Decision-Making
Risk aversion describes a preference for a certain outcome over a gamble with the same expected value. A risk-averse player will choose a smaller, certain payoff over a larger, uncertain payoff with the same expected value. Conversely, a risk-neutral player is indifferent between the two. A risk-seeking player prefers the gamble. Example:Consider two options:* Option A: Receive $100 with certainty.
Option B
Receive $200 with probability 0.5, and $0 with probability 0.5.Both options have an expected value of $100. A risk-averse player would choose Option A, while a risk-neutral player would be indifferent, and a risk-seeking player would choose Option B. Mathematically, this can be modeled using utility functions, where a risk-averse player’s utility function is concave.
Robust Game Theory and Model Uncertainty
Robust game theory tackles the issue of model uncertainty, acknowledging that the true game being played might not perfectly match the model. It focuses on finding strategies that perform well across a range of possible models or scenarios. This approach helps to mitigate the risks associated with relying on a single, potentially inaccurate model.
Game Theory and Cooperation
Game theory, my dear students, often paints a picture of ruthless competition, a battlefield of self-interest. Yet, within its elegant framework lies the capacity to illuminate the subtle dance of cooperation, a phenomenon as vital to human society as the very air we breathe. It reveals how cooperation, far from being a naive ideal, can emerge strategically, even amidst competing desires.
We will explore how game theory models this fascinating interplay, examining both its triumphs and limitations in explaining the complex tapestry of human interaction.The core of understanding cooperation within game theory lies in recognizing that the “best” strategy for an individual isn’t always pure selfishness. Sometimes, mutual benefit arises from coordinated actions, creating a scenario where cooperation leads to a superior outcome for all involved compared to individualistic pursuits.
This is beautifully illustrated in various game theory models, such as the Prisoner’s Dilemma, where cooperation, although risky, can lead to better results than the inevitable mutual betrayal that often ensues.
The Prisoner’s Dilemma and its Cooperative Solutions
The Prisoner’s Dilemma, a cornerstone of game theory, presents a scenario where two individuals, facing potential imprisonment, must decide whether to cooperate (remain silent) or defect (betray the other). If both cooperate, they receive a light sentence. If both defect, they receive a harsher sentence. However, if one defects while the other cooperates, the defector goes free while the cooperator receives a severe punishment.
This creates a tension: the rational self-interest of each individual leads to mutual defection, a worse outcome than if they had cooperated. However, repeated iterations of the game, introducing the possibility of future interactions, show that cooperative strategies, like “tit-for-tat,” can emerge and become stable, proving that cooperation can be a winning strategy in the long run. This highlights the importance of repeated interactions and the shadow of the future in fostering cooperation.
Game Theory’s Success in Predicting Cooperative Outcomes
Game theory has accurately predicted cooperative behavior in various real-world situations. For instance, international arms control agreements, though often fraught with challenges, can be seen as examples of cooperative outcomes influenced by the principles of game theory. Nations, understanding the potential for mutually destructive conflict, often find it strategically advantageous to negotiate arms limitations, even if complete disarmament remains elusive.
Similarly, the success of many international trade agreements, which involve cooperation between nations to reduce trade barriers and increase mutual economic benefits, can be partly attributed to an understanding of the strategic incentives for cooperation. These agreements demonstrate how game theory can predict and even help design cooperative outcomes.
Limitations of Game Theory in Modeling Complex Cooperation
While game theory provides valuable insights into cooperation, its limitations become apparent when dealing with the complexities of real-world interactions. Simple models often oversimplify human behavior, neglecting factors like altruism, trust, social norms, and the influence of emotions. Furthermore, the assumption of perfect rationality, a cornerstone of many game-theoretic models, often fails to capture the nuances of human decision-making.
In situations involving large numbers of participants, the complexity of interactions can overwhelm even the most sophisticated models, making accurate predictions challenging. The evolution of cooperation in complex systems, for instance, often involves mechanisms beyond simple strategic interactions, such as reputation, social learning, and the emergence of social norms, which are difficult to fully capture within traditional game-theoretic frameworks.
Game Theory and Conflict
Game theory, a powerful analytical tool, offers valuable insights into the dynamics of conflict. By modeling interactions between actors with conflicting interests, it helps us understand the strategic choices they make, the potential outcomes, and the factors that influence these outcomes. This exploration delves into the core concepts, empirical examples, limitations, and future directions of game theory in the context of conflict.
Game Theory Models Applicable to Conflict Analysis
Several game theory models provide frameworks for analyzing conflict. Understanding their structure—players, strategies, and payoffs—and their Nash Equilibria is crucial for predicting conflict outcomes. The Nash Equilibrium represents a stable state where no player can improve their outcome by unilaterally changing their strategy, given the other players’ strategies. However, it doesn’t necessarily indicate a desirable or efficient outcome.
- Prisoner’s Dilemma: Two suspects are arrested and interrogated separately. Each can either confess or remain silent. The payoff matrix shows that mutual silence leads to a relatively light sentence, while mutual confession leads to a harsher sentence for both. However, confessing while the other remains silent yields the best outcome for the confessor. The Nash Equilibrium is mutual confession, even though mutual silence would be a better outcome for both.
Payoff Matrix: (Confess, Confess) = (-5, -5); (Confess, Silent) = (0, -10); (Silent, Confess) = (-10, 0); (Silent, Silent) = (-1, -1).
- Chicken: Two drivers speed toward each other. The first to swerve is considered the “chicken,” while the other wins. The Nash Equilibrium is a mixed-strategy equilibrium, where each player has a probability of swerving and a probability of not swerving. Payoff Matrix: (Swerve, Swerve) = (0, 0); (Swerve, Straight) = (-1, 1); (Straight, Swerve) = (1, -1); (Straight, Straight) = (-10, -10).
- Stag Hunt: Two hunters can cooperate to hunt a stag (high payoff) or hunt a hare individually (moderate payoff). If one hunts a stag and the other a hare, the stag hunter gets nothing. The Nash Equilibria are (Stag, Stag) and (Hare, Hare). The (Stag, Stag) equilibrium is Pareto efficient, but requires trust and coordination. Payoff Matrix: (Stag, Stag) = (10, 10); (Stag, Hare) = (0, 5); (Hare, Stag) = (5, 0); (Hare, Hare) = (5, 5).
- Assurance Game: Two players must simultaneously decide whether to cooperate or defect. If both cooperate, they receive a high payoff; if both defect, they receive a low payoff. If one cooperates and the other defects, the cooperator receives a low payoff and the defector a high payoff. The Nash Equilibria are (Cooperate, Cooperate) and (Defect, Defect). Payoff Matrix: (Cooperate, Cooperate) = (5, 5); (Cooperate, Defect) = (0, 10); (Defect, Cooperate) = (10, 0); (Defect, Defect) = (1, 1).
Factors Influencing Conflict Outcomes
Several factors beyond the basic game structure significantly influence conflict outcomes. These factors introduce complexities and uncertainties, making accurate predictions challenging.
- Information Asymmetry: Unequal access to information can lead to miscalculations and escalation. For example, a country unaware of another’s military capabilities might misjudge the risks of conflict.
- Commitment and Credibility: Credible threats or commitments can deter adversaries. A strong reputation for following through on threats enhances credibility. Signaling, through actions or statements, can convey intentions and influence opponent behavior.
- Third-Party Intervention: Mediators or arbitrators can facilitate communication, propose solutions, and alter power dynamics, often leading to peaceful resolutions.
- Risk Aversion/Preference: Risk-averse actors are less likely to escalate conflicts, preferring certain, though potentially less advantageous, outcomes. Risk-seeking actors, conversely, might gamble on higher potential payoffs, even if it increases the risk of significant losses.
Successful Predictions of Conflict Outcomes
Game theory has successfully predicted or explained the outcomes of several conflicts.
- The Cuban Missile Crisis (1962): Modeled as a Prisoner’s Dilemma, both the US and USSR faced the choice of escalating or de-escalating. The predicted outcome, a negotiated settlement, aligned with the actual outcome. The high cost of nuclear war made mutual cooperation (de-escalation) a rational choice, despite the inherent distrust.
- Arms Races: The dynamics of arms races can be analyzed using the Prisoner’s Dilemma. Each nation has an incentive to increase its military capabilities, even though the overall outcome is a costly and potentially dangerous arms race. Game theory helps explain why arms races often occur despite their negative consequences.
- The Cold War: Elements of the Assurance Game and the Stag Hunt can be seen in the Cold War. The possibility of mutually assured destruction incentivized cooperation (avoiding direct conflict), but the inherent distrust and competition led to a prolonged period of tension and proxy wars.
Case Study Table
| Conflict Name | Game Theory Model Applied | Predicted Outcome | Actual Outcome | Accuracy Assessment | Limitations |
|---|---|---|---|---|---|
| Cuban Missile Crisis | Prisoner’s Dilemma | Negotiated settlement | Negotiated settlement | High | Simplified representation of complex motivations |
| Arms Race (Cold War) | Prisoner’s Dilemma | Escalation of arms buildup | Escalation of arms buildup | High | Oversimplification of factors influencing decision-making |
| Cold War (overall) | Assurance Game/Stag Hunt | Prolonged tension, proxy conflicts, eventual de-escalation | Prolonged tension, proxy conflicts, eventual de-escalation | Moderate | Difficulty in assigning precise payoffs to complex geopolitical factors |
Limitations of Game Theory in Predicting Conflict Dynamics
While game theory offers valuable insights, it has limitations in accurately predicting conflict dynamics.
- Simplifying Assumptions: Game theory models often assume rationality and complete information, which rarely holds true in real-world conflicts. Emotions, irrationality, and unforeseen events significantly influence outcomes.
- Difficulty in Assigning Payoffs: Quantifying the payoffs associated with conflict outcomes is challenging. Factors like national security, public opinion, and ideological commitments are difficult to translate into numerical values.
- Escalation Dynamics: Game theory struggles to capture the complex processes of conflict escalation, including the influence of psychological factors, power imbalances, and social norms.
Evolutionary Game Theory and Conflict
Evolutionary game theory extends traditional game theory by incorporating concepts of adaptation and selection. It helps explain how strategies evolve over time based on their success in repeated interactions. This approach offers a more nuanced understanding of conflict dynamics, particularly in situations with incomplete information or evolving player behavior.
Game Theory and Negotiation
Game theory provides a framework for analyzing negotiation strategies. By understanding the potential payoffs associated with different outcomes, negotiators can develop strategies to achieve mutually beneficial agreements and avoid conflict escalation. Concepts like the Nash Bargaining Solution offer insights into efficient and fair outcomes in negotiations.
FAQ Section
What are some common misconceptions about game theory?
A common misconception is that game theory always predicts perfectly. In reality, its accuracy depends heavily on the assumptions made and the complexity of the situation. Another is that game theory only applies to simple, stylized games; it’s increasingly used to model complex real-world scenarios.
How does game theory differ from other predictive methods?
Game theory uniquely focuses on strategic interactions between rational agents. Unlike statistical models that predict outcomes based on historical data, game theory attempts to predict outcomes based on the anticipated actions of players considering each other’s strategies.
Can game theory be used to predict individual behavior?
While game theory primarily models interactions between agents, insights from behavioral game theory can offer a better understanding of individual decision-making under strategic considerations, though perfect prediction of individual behavior remains a challenge.
What are the ethical implications of using game theory for prediction?
Ethical concerns arise when game theory predictions are used to manipulate outcomes, particularly in situations with significant societal impact. Transparency and responsible application are crucial to avoid potential misuse.


