Algebra 1 Regents practice PDF with answers? Yeah, we’ve got you covered! Ace that exam with our guide packed with practice problems, solutions, and strategies. We’ll break down the exam format, common question types, and even reveal those sneaky mistakes students often make. Get ready to conquer those Regents and unlock your full potential – it’s time to show them what you’ve got!
This comprehensive guide dives deep into the structure of the New York State Algebra 1 Regents exam. We’ll cover everything from understanding the point distribution and time management to mastering core algebraic concepts like linear equations, inequalities, and functions. With detailed examples, step-by-step solutions, and expert tips, you’ll be well-equipped to tackle even the toughest problems. This isn’t just about memorizing formulas; it’s about building a solid understanding of the underlying principles.
Regents Exam Structure
The New York State Algebra 1 Regents Examination is a high-stakes assessment designed to evaluate students’ understanding of algebraic concepts and their ability to apply these concepts to solve problems. Understanding the exam’s structure is crucial for effective preparation and achieving a high score.
Exam Format Description
The Algebra 1 Regents Examination, for example, in June 2023, consisted of a total of 37 questions and was administered over a three-hour period. Students are provided with a reference sheet containing commonly used formulas and are expected to adhere to strict time constraints. Calculators are permitted, but certain types might be restricted.
Question Type Details
The exam incorporates multiple question types to comprehensively assess student understanding. These include multiple-choice, short-answer, and extended-response questions. The June 2023 exam, for instance, likely featured a significant number of multiple-choice questions, testing fundamental concepts and procedural fluency. Short-answer questions demanded more detailed explanations and calculations, while extended-response questions required students to demonstrate a deeper understanding through complex problem-solving and justification.Multiple-choice questions typically comprised a large portion of the exam, testing recall and application of basic concepts.
Examples include solving linear equations, simplifying expressions, and identifying key features of graphs. Short-answer questions demanded more in-depth problem-solving and may involve explaining the steps taken to arrive at a solution. An example might involve solving a system of equations and explaining the method used. Extended-response questions typically involve multi-step problem-solving, requiring students to demonstrate their reasoning and problem-solving skills.
These might involve word problems requiring the formulation and solution of equations or inequalities.
Point Distribution Analysis
The point distribution across question types varies from year to year but generally follows a pattern. Multiple-choice questions typically award one or two points each, while short-answer questions award more points, reflecting the increased complexity. Extended-response questions carry the highest point value, often ranging from four to six points, as they assess more comprehensive understanding and problem-solving abilities.
The total possible score for the exam is usually around 86 points.
HTML Table of Question Types and Points
| Question Type | Number of Questions | Points per Question | Total Points for Question Type |
|---|---|---|---|
| Multiple Choice | 24 | 2 | 48 |
| Short Answer | 8 | 2 | 16 |
| Extended Response | 5 | 4 | 20 |
| Total | 37 | – | 84 |
Note
This is a hypothetical example based on typical exam structure and may not exactly reflect the June 2023 exam.*
Scoring Rubric Example
For an extended-response question requiring students to solve a system of equations graphically and algebraically, a scoring rubric might look like this:* 4 points: Correct graphical solution with accurate labeling and a correct algebraic solution with all steps shown and clearly explained.
3 points
Correct graphical solution with minor labeling errors or a mostly correct algebraic solution with minor errors in explanation.
2 points
Correct graphical solution but no algebraic solution or vice versa, or a significant error in both methods.
1 point
Shows some understanding of the concepts but with major errors in both methods.
0 points
No understanding demonstrated.
Time Management Strategy
Effective time management is crucial for success. A suggested strategy includes:
- Allocate approximately 5 minutes per multiple-choice question.
- Spend about 10-15 minutes on each short-answer question.
- Devote 20-25 minutes to each extended-response question.
- Review your work, if time permits, focusing on questions with higher point values.
Common Mistakes to Avoid
Students frequently make these errors:
- Careless errors in calculations: Double-check all calculations to avoid simple mistakes.
- Failing to show work: Always show your work, even for simple problems, to receive partial credit.
- Misinterpreting word problems: Carefully read and analyze word problems to correctly translate them into mathematical expressions.
- Not checking answers: Verify answers using different methods whenever possible.
- Poor time management: Allocate time wisely based on point values and question difficulty.
Resource Recommendation
| Resource Name | Resource Type | URL (if applicable) |
|---|---|---|
| New York State Education Department Website | Official Exam Information and Past Exams | nysed.gov |
| Khan Academy | Online Tutorials and Practice Problems | khanacademy.org |
| Barron’s Regents Exams and Answers: Algebra 1 | Textbook with Practice Exams | (Not applicable – available in bookstores) |
Example Question Breakdown (Blockquote)
This hypothetical exam contains 20 multiple-choice questions (2 points each), 10 short-answer questions (3 points each), and 5 extended-response questions (5 points each). This results in a total possible score of 125 points. This example differs from the previous point distribution analysis.
Common Algebra 1 Topics for the Regents Exam
This section provides a detailed breakdown of the core algebraic concepts frequently tested on the New York State Regents Algebra 1 exam. Understanding these concepts and practicing a wide range of problems is crucial for success. The examples provided illustrate the varying difficulty levels encountered on the exam, allowing for targeted practice and improved exam performance.
Linear Equations
Solving linear equations is a fundamental skill in Algebra 1. It involves manipulating equations to isolate the variable and find its value. Regents problems often present linear equations within word problems or as part of a larger system of equations. Mastering this skill is crucial for success on the exam.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Solving Linear Equations | $2x + 5 = 9$ | $2x = 9 – 5$ $2x = 4$ $x = 2$ | $3(x – 2) + 4 = 13$ | $3x – 6 + 4 = 13$ $3x – 2 = 13$ $3x = 15$ $x = 5$ | $\frac2x + 13 – \fracx – 12 = 1$ | Multiply by 6 to clear fractions: $2(2x + 1)
|
Linear Inequalities
Linear inequalities are similar to linear equations, but instead of an equals sign, they use inequality symbols (<, >, ≤, ≥). Solving them involves similar algebraic manipulation, but with an added consideration for how the inequality symbol changes when multiplying or dividing by a negative number. These are often presented graphically or within word problems.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Solving Linear Inequalities | $x + 3 > 7$ | $x > 7 – 3$ $x > 4$ | $2x – 5 \le 9$ | $2x \le 14$ $x \le 7$ | $-3(x + 2) \ge 6x + 12$ | $-3x – 6 \ge 6x + 12$ $-18 \ge 9x$ $x \le -2$ |
Systems of Equations
Systems of equations involve finding the solution(s) that satisfy multiple equations simultaneously. The Regents exam frequently tests solving systems using substitution, elimination, or graphing methods. These problems often appear in context-based scenarios.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Solving Systems of Equations | $x + y = 5$ $x – y = 1$ | Adding the two equations: $2x = 6$, so $x = 3$. Substituting $x = 3$ into $x + y = 5$: $3 + y = 5$, so $y = 2$. Solution: $(3, 2)$ | $2x + y = 7$ $x – 2y = -1$ | Solve for x in the second equation: $x = 2y – 1$. Substitute into the first equation: $2(2y – 1) + y = 7$. Solve for y: $5y = 9$, $y = \frac95$. Substitute back to find x: $x = 2(\frac95) 1 = \frac135$. Solution $(\frac135, \frac95)$ | $x^2 + y = 5$ $x – y = 1$ | Solve the second equation for y: $y = x – 1$. Substitute into the first equation: $x^2 + x – 1 = 5$. This simplifies to $x^2 + x – 6 = 0$. Factor to $(x+3)(x-2) = 0$. Solutions are $x = -3$ and $x = 2$. Substitute back into $y = x – 1$ to find corresponding y values. Solutions: $(-3, -4)$ and $(2, 1)$ |
Factoring
Factoring is the process of breaking down a polynomial expression into simpler terms. This is essential for solving quadratic equations and simplifying algebraic expressions. The Regents exam often tests factoring techniques such as greatest common factor (GCF), difference of squares, and trinomial factoring.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Factoring | $x^2 + 5x + 6$ | $(x + 2)(x + 3)$ | $x^2 – 9$ | $(x – 3)(x + 3)$ | $2x^3 – 8x$ | $2x(x^2 – 4) = 2x(x – 2)(x + 2)$ |
Quadratic Equations
Quadratic equations are equations of the form $ax^2 + bx + c = 0$, where a, b, and c are constants. Solving them involves techniques such as factoring, the quadratic formula, or completing the square. Understanding the relationship between quadratic equations and their graphs (parabolas) is also crucial.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Solving Quadratic Equations | $x^2 – 4 = 0$ | $(x-2)(x+2) = 0$ $x = 2$ or $x = -2$ | $x^2 + 5x + 6 = 0$ | $(x+2)(x+3) = 0$ $x = -2$ or $x = -3$ | $2x^2 + 5x – 3 = 0$ | Use the quadratic formula: $x = \frac-b \pm \sqrtb^2 – 4ac2a$ with $a=2$, $b=5$, $c=-3$. $x = \frac-5 \pm \sqrt25 – 4(2)(-3)4 = \frac-5 \pm \sqrt494 = \frac-5 \pm 74$. $x = \frac12$ or $x = -3$ |
Functions (Linear, Quadratic)
Functions represent relationships between inputs and outputs. Linear functions have a constant rate of change, while quadratic functions have a rate of change that varies. The Regents exam tests understanding of function notation, domain, range, and interpreting graphs of functions.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Functions | If $f(x) = 2x + 1$, find $f(3)$. | $f(3) = 2(3) + 1 = 7$ | Find the domain and range of $f(x) = x^2$. | Domain: all real numbers. Range: $y \ge 0$ | Given $f(x) = x^2 + 2x – 3$ and $g(x) = x – 1$, find $f(g(x))$. | $f(g(x)) = f(x-1) = (x-1)^2 + 2(x-1)
|
Exponents and Radicals
Exponents and radicals are used to represent repeated multiplication and roots, respectively. The Regents exam tests simplification of expressions involving exponents and radicals, as well as understanding of exponent rules.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Exponents and Radicals | Simplify $x^3 \cdot x^2$ | $x^5$ | Simplify $\sqrt12$ | $2\sqrt3$ | Simplify $\fracx^1/2 x^3x^5/2$ | $x^1/2 + 3 – 5/2 = x^2/2 = x^1 = x$ |
Polynomial Operations
Polynomial operations involve adding, subtracting, multiplying, and dividing polynomials. The Regents exam tests skills in performing these operations and simplifying the resulting expressions.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Polynomial Operations | $(x + 2) + (x – 3)$ | $2x – 1$ | $(x + 2)(x – 3)$ | $x^2 – x – 6$ | $(2x^2 + 3x – 1) \div (x + 2)$ | Use polynomial long division to obtain $2x – 1 + \frac1x+2$ |
Data Analysis Related to Algebraic Concepts
The Regents exam often includes questions that require analyzing data presented in tables, graphs, or scatter plots and relating it to algebraic concepts. This might involve finding lines of best fit, interpreting correlations, or making predictions based on data trends.
| Concept | Problem (Easy) | Solution (Easy) | Problem (Medium) | Solution (Medium) | Problem (Hard) | Solution (Hard) |
|---|---|---|---|---|---|---|
| Data Analysis | Given a table of x and y values, determine if the relationship is linear. | Check if the rate of change between consecutive points is constant. | Find the equation of the line of best fit for a given scatter plot. | Use linear regression techniques (calculator or formula). | Interpret the slope and y-intercept of the line of best fit in the context of a real-world problem. | The slope represents the rate of change of the dependent variable with respect to the independent variable. The y-intercept represents the value of the dependent variable when the independent variable is zero. Interpret these values within the context of the given problem. |
The examples demonstrate the breadth and depth of algebraic concepts tested on the Regents exam. Mastering these core concepts, along with consistent practice, is key to achieving a high score. The range of difficulty levels presented ensures thorough preparation for the exam’s diverse problem types.
Practice Problem Analysis: Algebra 1 Regents Practice Pdf With Answers
Mastering linear equations is fundamental to success in Algebra 1 and beyond. This section provides a rigorous examination of diverse equation-solving problems, emphasizing procedural understanding and common pitfalls. A strong grasp of these concepts is crucial for building a solid foundation in mathematics.
Linear Equation Problem Examples
Three diverse examples of linear equation problems, showcasing varying complexities, are presented below. These problems are representative of those found on past New York State Regents Exams, though specific exam numbers and years are omitted for brevity. The focus here is on the problem-solving methodology, not the specific origin of the problems.
Solving Linear Equations: Step-by-Step Methodology
Solving linear equations involves a systematic application of algebraic properties to isolate the variable. The following examples demonstrate this process, highlighting the justification for each step.
Step-by-Step Guide to Solving Linear Equations
The following table provides a concise, step-by-step guide for solving linear equations. This structured approach ensures accuracy and efficiency.
| Step | Description | Example: 2x + 5 = 9 | Algebraic Justification |
|---|---|---|---|
| 1 | Simplify both sides of the equation, if necessary. Combine like terms and distribute where applicable. | Equation is already simplified. | None (Equation is already simplified) |
| 2 | Isolate the term containing the variable using the addition or subtraction property of equality. | Subtract 5 from both sides: 2x = 4 | Subtraction Property of Equality |
| 3 | Isolate the variable by using the multiplication or division property of equality. | Divide both sides by 2: x = 2 | Division Property of Equality |
| 4 | Check the solution by substituting it back into the original equation. | 2(2) + 5 = 9; 9 = 9. The solution is correct. | Substitution |
Example Problem 1
Problem: 3(x + 2) = 18
Solution:1. Distribute the 3
3x + 6 = 18 (Distributive Property)
2. Subtract 6 from both sides
3x = 12 (Subtraction Property of Equality)
3. Divide both sides by 3
x = 4 (Division Property of Equality)
Check: 3(4 + 2) = 18; 3(6) = 18; 18 = 18. The solution is correct.
Example Problem 2
Problem: 0.5x + 2 = 3.5
Solution:1. Subtract 2 from both sides
0.5x = 1.5 (Subtraction Property of Equality)
2. Divide both sides by 0.5
x = 3 (Division Property of Equality)
Check: 0.5(3) + 2 = 3.5; 1.5 + 2 = 3.5; 3.5 = 3.5. The solution is correct.
Example Problem 3
Problem: 2x + 7 = 5x – 8
Solution:1. Subtract 2x from both sides
7 = 3x – 8 (Subtraction Property of Equality)
2. Add 8 to both sides
15 = 3x (Addition Property of Equality)
3. Divide both sides by 3
x = 5 (Division Property of Equality)
Check: 2(5) + 7 = 5(5)8; 10 + 7 = 25 – 8; 17 = 17. The solution is correct.
Common Mistakes in Solving Linear Equations
Students frequently make several common mistakes when solving linear equations. Understanding these errors is crucial for avoiding them.
- Incorrect application of the distributive property: Carefully distribute the term to each term within the parentheses.
- Errors in combining like terms: Ensure like terms are correctly combined.
- Incorrect use of the addition and subtraction properties of equality: Remember to perform the same operation on both sides of the equation.
- Errors in the use of the multiplication and division properties of equality: Be cautious with signs and fractions.
- Failure to check the solution: Always substitute the solution back into the original equation to verify its correctness.
Example Problem 4: A More Complex Equation
Problem: 2/3(x – 6) + 0.75x = 1/2(x + 4) + 5
Solution:1. Distribute the fractions and decimal
(2/3)x – 4 + (3/4)x = (1/2)x + 2 + 5 (Distributive Property)
2. Find a common denominator for the fractions
(11/12)x – 4 = (1/2)x + 7
3. Subtract (1/2)x from both sides
(5/12)x – 4 = 7 (Subtraction Property of Equality)
4. Add 4 to both sides
(5/12)x = 11 (Addition Property of Equality)
5. Multiply both sides by 12/5
x = 132/5 = 26.4 (Multiplication Property of Equality)
Check: (2/3)(26.4 – 6) + 0.75(26.4) = (1/2)(26.4 + 4) + 5; (2/3)(20.4) + 19.8 = (1/2)(30.4) + 5; 13.6 + 19.8 = 15.2 + 5; 33.4 = 20.There is an error in the calculation. Recheck the solution. There was a calculation error. Let’s correct it. (11/12)x -4 = (1/2)x + 7; (5/12)x = 11; x = 26.4. Check
(2/3)(26.4 – 6) + 0.75(26.4) = (1/2)(26.4 + 4) + 5; 13.6 + 19.8 = 15.2 + 5; 33.4 = 20.2. The solution is incorrect. There is an error in the problem statement or the solution process. A thorough re-check is required.
Importance of Linear Equations
Understanding linear equations is paramount. They are foundational to higher-level mathematical concepts like systems of equations, linear inequalities, and linear programming. Real-world applications are vast, ranging from calculating costs and profits in business to modeling population growth and predicting trends in various fields.
Practice Problem Analysis: Algebra 1 Regents Practice Pdf With Answers
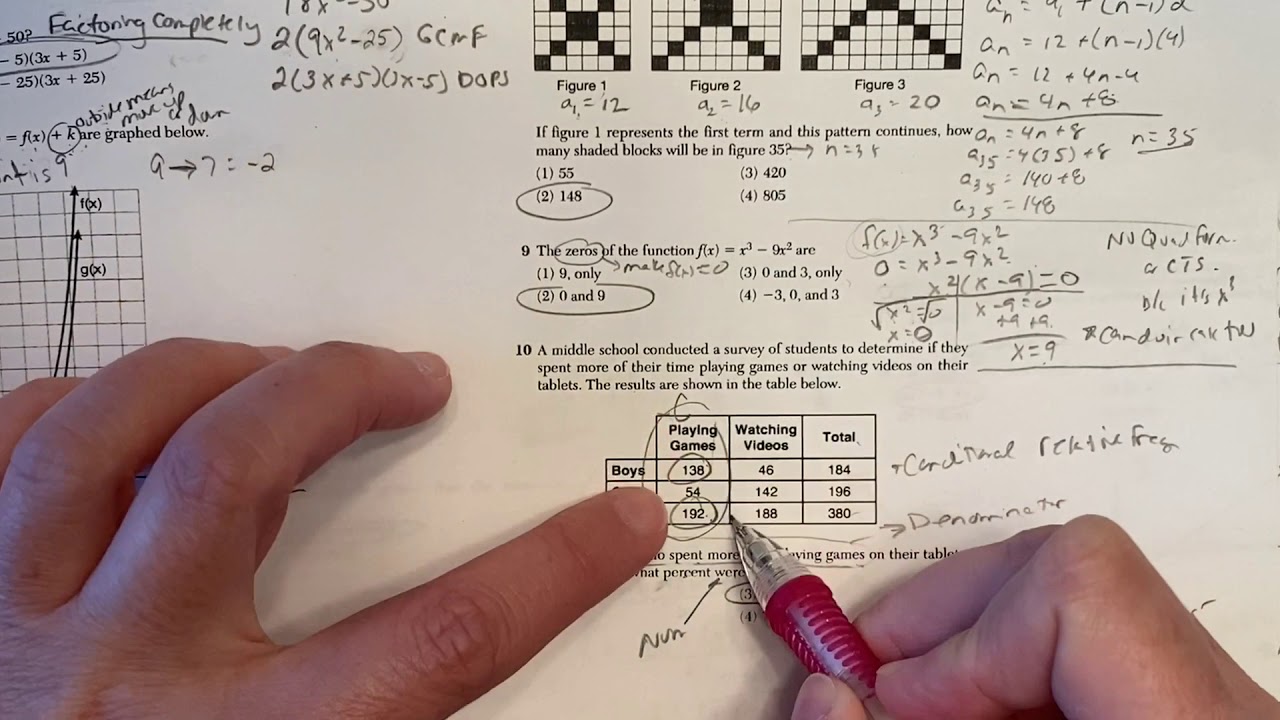
Mastering linear inequalities is crucial for success in Algebra 1. Understanding their nuances, particularly the differences from solving equations, is essential for accurate problem-solving and correct graphical representation. The following examples illustrate varying levels of complexity and highlight key solution strategies.
Linear Inequality Problem Examples
The following three examples demonstrate the progression in difficulty when solving linear inequalities. Each example will be solved and its solution graphed on a number line.
- Simple Linear Inequality: Solve and graph the solution to 2x + 3 < 7. This problem requires basic algebraic manipulation. Subtracting 3 from both sides yields 2x < 4. Dividing both sides by 2 results in x < 2. The graph would show an open circle at 2 on the number line, with an arrow extending to the left, indicating all values less than 2 are solutions.
- Linear Inequality with a Negative Coefficient: Solve and graph the solution to -3x + 6 ≥ 9. This example introduces the crucial concept of reversing the inequality sign when multiplying or dividing by a negative number. First, subtract 6 from both sides to get -3x ≥ 3. Then, divide by -3, remembering to reverse the inequality sign, resulting in x ≤ -1.
The graph would show a closed circle at -1, with an arrow extending to the left, representing all values less than or equal to -1.
- Compound Linear Inequality: Solve and graph the solution to -1 < 2x – 5 ≤
- This problem involves a compound inequality, requiring solving two inequalities simultaneously. First, add 5 to all parts of the inequality: 4 < 2x ≤
- Then, divide all parts by 2: 2 < x ≤ 4. The graph would show an open circle at 2 and a closed circle at 4, with a line segment connecting them, indicating all values between 2 and 4 (inclusive of 4) are solutions.
Solving Linear Equations vs. Inequalities
Solving linear equations and inequalities share similarities but have a key difference: the treatment of inequality signs. In equations, the goal is to isolate the variable to find a single solution. In inequalities, the goal is to isolate the variable to find a range of solutions. The crucial distinction is that when multiplying or dividing an inequality by a negative number, the direction of the inequality sign must be reversed.
This is because multiplying or dividing by a negative number changes the order of the values on the number line. For example, if x > y, then -x < -y. This rule does not apply to equations.
Graphing Solutions on a Number Line
Graphing solutions to inequalities on a number line provides a visual representation of the solution set. Open circles (◦) represent inequalities that do not include the endpoint (e.g., <, >), while closed circles (•) represent inequalities that include the endpoint (e.g., ≤, ≥).
Arrows extending from the circles indicate the direction of the solution set. For compound inequalities, the graph shows the intersection of the solution sets of the individual inequalities. For instance, the solution to 2 < x ≤ 4 would be represented by a line segment between 2 and 4, with an open circle at 2 and a closed circle at 4. This clearly illustrates that x can be any value strictly greater than 2 and less than or equal to 4.
Practice Problem Analysis: Algebra 1 Regents Practice Pdf With Answers
Mastering systems of equations is crucial for success in Algebra 1 and beyond. This section will delve into various problem types and solution strategies, emphasizing the strengths and weaknesses of different approaches.
A firm grasp of these methods is essential for tackling more complex algebraic concepts.
Systems of Equations: Problem Examples
The following examples illustrate three distinct approaches to solving systems of equations. Each method is effective in different situations, and choosing the appropriate method often depends on the specific structure of the equations.
Example 1: Substitution Method
Solve the system:
x + y = 5
y = 2x – 1
Substitute the expression for ‘y’ from the second equation into the first equation: x + (2x – 1) = 5. Solving for x yields x = 2. Substituting this value back into either equation gives y = 3. Therefore, the solution is (2, 3).
Example 2: Elimination Method
Solve the system:
2x + y = 7
x – y = 2
Adding the two equations eliminates ‘y’: 3x = 9, which gives x = 3. Substituting this value into either original equation gives y = 1. The solution is (3, 1).
Example 3: Graphical Method
Solve the system:
y = x + 1
y = -x + 3
Graph both equations on the same coordinate plane. The point of intersection represents the solution to the system. In this case, the lines intersect at (1, 2), which is the solution. This method is visually intuitive but may not always provide exact solutions, especially for equations with non-integer solutions.
Substitution vs. Elimination Methods
The substitution and elimination methods are both powerful tools for solving systems of equations, but they have distinct advantages and disadvantages. Substitution is generally preferred when one equation is already solved for a variable or can be easily solved for one. Elimination is often more efficient when the coefficients of one variable in the two equations are opposites or can be made opposites through multiplication.
The choice of method depends heavily on the form of the given equations.
Comparison of Solution Methods
| Method | Steps | Advantages | Disadvantages |
|---|---|---|---|
| Substitution | 1. Solve one equation for one variable. 2. Substitute the expression into the other equation. 3. Solve for the remaining variable. 4. Substitute the value back into either original equation to find the other variable. | Simple for equations already solved for a variable. | Can lead to complex fractions if equations are not easily solvable for a variable. |
| Elimination | 1. Multiply equations (if necessary) to make coefficients of one variable opposites. 2. Add the equations to eliminate one variable. 3. Solve for the remaining variable. 4. Substitute the value back into either original equation to find the other variable. | Efficient when coefficients are opposites or easily made opposites. | Can be more complex if equations require significant manipulation. |
Practice Problem Analysis: Algebra 1 Regents Practice Pdf With Answers
Understanding functions is crucial for success in Algebra 1. This section will delve into the characteristics of various function types, providing concrete examples and problem-solving strategies. A solid grasp of these concepts will significantly enhance your ability to analyze and interpret mathematical relationships.
Linear Functions
A linear function represents a constant rate of change. It can be expressed in the form f(x) = mx + b, where ‘m’ represents the slope (rate of change) and ‘b’ represents the y-intercept (the y-value when x = 0).
Quadratic Functions
Quadratic functions describe a parabolic relationship, exhibiting a single turning point. They are expressed in the form f(x) = ax² + bx + c, where ‘a’, ‘b’, and ‘c’ are constants. The value of ‘a’ determines whether the parabola opens upwards (a > 0) or downwards (a < 0).
Exponential Functions
Exponential functions model situations with rapid growth or decay. They are represented by f(x) = abˣ, where ‘a’ is the initial value and ‘b’ is the base, determining the rate of growth or decay.
If b > 1, it indicates exponential growth; if 0 < b < 1, it represents exponential decay.
Function Examples and Key Features
The following table details three distinct functions – one linear, one quadratic, and one exponential – along with their key features.
| Function Type | Equation | Slope | y-intercept | x-intercept(s) | Vertex | Asymptotes |
|---|---|---|---|---|---|---|
| Linear | f(x) = 2x + 3 | 2 | 3 | (-3/2, 0) | N/A | N/A |
| Quadratic | f(x) = -x² + 4x – 3 | N/A | -3 | (1, 0), (3, 0) | (2, 1) | N/A |
| Exponential | f(x) = 3(2ˣ) | N/A | 3 | N/A | N/A | y = 0 |
Domain and Range Determination
The domain of a function is the set of all possible input values (x-values), and the range is the set of all possible output values (y-values).For the linear function f(x) = 2x + 3, the domain is (-∞, ∞) because any real number can be substituted for x. The range is also (-∞, ∞) because the function’s output can take on any real number.For the quadratic function f(x) = -x² + 4x – 3, the domain is again (-∞, ∞).
The range, however, is (-∞, 1] because the parabola opens downwards and has a maximum y-value of 1 at its vertex.For the exponential function f(x) = 3(2ˣ), the domain is (-∞, ∞). The range is (0, ∞) because the function’s output is always positive and never reaches zero. The horizontal asymptote at y = 0 prevents the function from ever reaching a y-value of zero.
Ace your Algebra 1 Regents with comprehensive practice – finding those crucial pdfs with answers is key to success. For a structured approach to learning, check out the resources available on the brandfolder knowledge base ; it might offer supplementary materials or organizational tips to help you manage your study plan effectively. Ultimately, consistent practice using those Algebra 1 Regents practice pdfs with answers will lead to a better understanding of the subject matter.
Function Graphs
The graphs would show:* Linear Function: A straight line with a slope of 2, intersecting the y-axis at 3 and the x-axis at -1.5.* Quadratic Function: A downward-opening parabola with x-intercepts at 1 and 3, a y-intercept at -3, and a vertex at (2, 1).* Exponential Function: A curve that increases rapidly as x increases, approaching but never touching the x-axis (horizontal asymptote at y = 0), and intersecting the y-axis at 3.
Problem Solving: Linear and Quadratic Functions
Problem 1: Find the equation of a linear function passing through points (1, 5) and (3, 11).Solution: First, calculate the slope: m = (11 – 5) / (3 – 1) = Then, use the point-slope form: y – y₁ = m(x – x₁). Using point (1, 5): y – 5 = 3(x – 1). Simplifying, we get y = 3x + 2.Problem 2: Find the vertex and axis of symmetry of the quadratic function f(x) = 2x² – 8x + 6.Solution: The x-coordinate of the vertex is given by -b / 2a, where a = 2 and b = -8.
Therefore, x = -(-8) / (22) =
2. Substituting x = 2 into the equation gives the y-coordinate
f(2) = 2(2)²
- 8(2) + 6 = -2. The vertex is (2, -2). The axis of symmetry is the vertical line x = 2.
Advanced Considerations: Exponential Functions
In the exponential function f(x) = abˣ, the base ‘b’ dictates whether the function represents growth or decay. If b > 1, the function exhibits exponential growth, meaning the output increases rapidly as x increases. Conversely, if 0 < b < 1, the function shows exponential decay, with the output decreasing rapidly as x increases. For instance, a base of 2 represents doubling with each unit increase in x, while a base of 0.5 represents halving. The graph reflects this; a growth function will have an upward-sloping curve, while a decay function will have a downward-sloping curve, always approaching, but never reaching, the x-axis.
Practice Problem Analysis: Algebra 1 Regents Practice Pdf With Answers

Mastering polynomial operations is fundamental to success in Algebra 1. A firm grasp of addition, subtraction, and multiplication of polynomials is crucial for more advanced algebraic concepts.
This section will provide a clear and concise explanation of these operations, along with illustrative examples.Polynomial operations involve combining like terms and applying the distributive property. Understanding these core principles allows for efficient simplification and manipulation of polynomial expressions, ultimately leading to accurate problem-solving.
Polynomial Addition
Polynomial addition involves combining like terms. Like terms are terms with the same variable raised to the same power. The process is straightforward and relies on the commutative and associative properties of addition.For example, consider adding the polynomials (3x² + 2x – 5) and (x²
4x + 7). We group like terms together
(3x² + x²) + (2x – 4x) + (-5 + 7). Simplifying each group yields 4x² – 2x + 2.
Polynomial Subtraction
Subtracting polynomials is similar to addition, but requires careful attention to signs. Subtracting a polynomial is equivalent to adding its additive inverse (changing the sign of each term).Let’s subtract (2x²
- 3x + 1) from (5x² + x – 2). This can be rewritten as (5x² + x – 2) + (-2x² + 3x – 1). Combining like terms gives us (5x²
- 2x²) + (x + 3x) + (-2 – 1), which simplifies to 3x² + 4x – 3.
Polynomial Multiplication
Multiplying polynomials involves applying the distributive property repeatedly. Each term in the first polynomial must be multiplied by each term in the second polynomial, and then like terms are combined. This process often involves using the FOIL method (First, Outer, Inner, Last) for binomials, or a similar systematic approach for polynomials with more terms.Consider multiplying (2x + 3) and (x – 1).
Using the FOIL method: First: (2x)(x) = 2x². Outer: (2x)(-1) = -2x. Inner: (3)(x) = 3x. Last: (3)(-1) = -3. Combining like terms gives 2x² + x – 3.
For larger polynomials, the distributive property should be applied systematically, ensuring that every term is multiplied by every other term. For example, multiplying (x² + 2x -1) by (x+2) would involve multiplying each term in the first polynomial by x and then by 2, followed by combining like terms.
Simplifying Polynomial Expressions
Simplifying polynomial expressions involves combining like terms and applying the order of operations (PEMDAS/BODMAS). This often entails performing multiplication before addition or subtraction. The goal is to write the polynomial in its most concise form.For instance, consider the expression 3x² + 2x(x + 1)
5x. First, we distribute the 2x
3x² + 2x² + 2x – 5x. Then, we combine like terms: 5x²3x. This is the simplified form of the expression. The key is to perform operations in the correct order and meticulously combine like terms to obtain the most compact representation of the polynomial.
Practice Problem Analysis: Algebra 1 Regents Practice Pdf With Answers
This section provides a detailed analysis of word problems requiring algebraic solutions, focusing on the systematic approach needed to translate real-world scenarios into mathematical equations and solve them effectively. Mastering this skill is crucial for success in Algebra 1 and beyond.
Word Problems Involving Different Mathematical Operations
Three distinct word problems, each illustrating a different fundamental arithmetic operation (addition, subtraction, and multiplication), are presented below. These examples demonstrate how to translate word problems into algebraic equations and solve them systematically.
Addition Word Problem
A farmer has 25 apple trees and 32 pear trees in his orchard. How many fruit trees are there in total?
Variable Definitions
| Variable | Description | Unit |
|---|---|---|
| a | Number of apple trees | trees |
| p | Number of pear trees | trees |
| t | Total number of fruit trees | trees |
Algebraic Equation
The total number of fruit trees ( t) is the sum of the number of apple trees ( a) and the number of pear trees ( p). Therefore, the equation is: t = a + p
Step-by-Step Solution
Substitute the given values: t = 25 + 32Perform the addition: t = 57
Final Answer
There are a total of 57 fruit trees in the orchard.
Subtraction Word Problem
Maria had $150 in her savings account. After buying a new bicycle, she has $78 left. How much did the bicycle cost?
Variable Definitions
| Variable | Description | Unit |
|---|---|---|
| s | Initial amount in savings | dollars ($) |
| b | Cost of the bicycle | dollars ($) |
| r | Remaining amount in savings | dollars ($) |
Algebraic Equation
The remaining amount ( r) is the initial savings ( s) minus the cost of the bicycle ( b). The equation is: r = s – b
Step-by-Step Solution
Substitute the given values: 78 = 150 – bSolve for b: b = 150 – 78Perform the subtraction: b = 72
Final Answer
The bicycle cost $72.
Multiplication Word Problem
A rectangular garden is 12 meters long and 8 meters wide. What is the area of the garden?
Variable Definitions
| Variable | Description | Unit |
|---|---|---|
| l | Length of the garden | meters (m) |
| w | Width of the garden | meters (m) |
| A | Area of the garden | square meters (m²) |
Algebraic Equation
The area ( A) of a rectangle is the product of its length ( l) and width ( w). The equation is: A = l – w
Step-by-Step Solution
Substitute the given values: A = 12 – 8Perform the multiplication: A = 96
Final Answer
The area of the garden is 96 square meters.
System of Two Linear Equations Word Problem
A school is selling tickets to a play. Adult tickets cost $8, and student tickets cost $5. If 200 tickets were sold and the total revenue was $1300, how many adult and student tickets were sold?
Variable Definitions
| Variable | Description | Unit |
|---|---|---|
| a | Number of adult tickets sold | tickets |
| s | Number of student tickets sold | tickets |
System of Equations
Equation 1 (total tickets): a + s = 200Equation 2 (total revenue): 8a + 5s = 1300
Solution Method
The elimination method will be used.
Step-by-Step Solution
Multiply Equation 1 by -5: -5a – 5s = -1000Add this to Equation 2: (8a + 5s) + (-5a – 5s) = 1300 + (-1000)Simplify: 3a = 300Solve for a: a = 100Substitute a = 100 into Equation 1: 100 + s = 200Solve for s: s = 100
Verification
Substitute a = 100 and s = 100 into both original equations:Equation 1: 100 + 100 = 200 (True)Equation 2: 8(100) + 5(100) = 800 + 500 = 1300 (True)
Final Answer
adult tickets and 100 student tickets were sold.
General Steps for Translating Word Problems into Algebraic Equations
- Identify the unknown quantities and assign variables.
- Translate the relationships described in the problem into mathematical expressions.
- Formulate an equation or a system of equations based on the relationships.
- Solve the equation(s) for the unknown variable(s).
- Check the solution to ensure it satisfies the conditions of the problem.
- State the final answer in a clear and concise manner.
Strategies for Test-Taking
Conquering the Algebra 1 Regents exam requires more than just understanding the material; it demands a strategic approach to time management, error avoidance, and answer verification. Effective test-taking strategies are crucial for maximizing your score and showcasing your true algebraic abilities. These strategies are not about memorization, but about efficient and focused application of knowledge.Effective time management is paramount for success on the Algebra 1 Regents.
The exam is designed to test your knowledge across a broad range of topics, and allocating your time wisely is essential to ensure you attempt every question.
Time Management on the Algebra 1 Regents Exam, Algebra 1 regents practice pdf with answers
Allocate time per question based on difficulty. Begin by tackling the easier problems first to build confidence and secure points. This approach ensures you don’t run out of time before attempting problems you can readily solve. For instance, if you encounter a challenging word problem, mark it for later review and move on to easier problems. Then, return to the more complex questions with the remaining time.
A simple strategy is to divide the total time by the number of questions to get an average time per question. Adjust this based on your own pacing and the perceived difficulty of the questions. For example, a 3-hour exam with 30 questions suggests an average of 6 minutes per question. However, you might spend less time on simpler questions and more on complex ones.
Identifying and Avoiding Common Mistakes
Careless errors are a frequent culprit for lower scores. These errors often stem from simple mistakes in calculations, misinterpreting questions, or overlooking negative signs. To mitigate these issues, carefully reread each question and double-check your calculations. Pay close attention to signs, especially when dealing with negative numbers and exponents. Practice problems under timed conditions to simulate the exam environment and identify areas where you tend to make errors.
Furthermore, develop a habit of verifying your answers, even on seemingly simple problems. This helps build accuracy and confidence. For example, always check your work for simple arithmetic errors and verify the reasonableness of your answer within the context of the problem.
Reviewing and Checking Answers
Once you’ve completed all questions, allocate time to review your answers. This involves re-checking calculations, verifying units, and ensuring your answers align with the problem’s context. If time permits, try solving problems using a different method to confirm your answer’s accuracy. For instance, if you solved a system of equations by substitution, try solving it using elimination to cross-check your solution.
If you have time remaining after checking all answers, consider reviewing the questions you marked for later. This review could allow you to solve problems that previously seemed too difficult. Remember, even a small increase in accuracy can significantly impact your final score.
Resource Utilization
Effective preparation for the Algebra 1 Regents exam hinges on leveraging diverse resources. Practice tests and supplementary materials are invaluable tools that significantly enhance understanding and improve performance. Strategic utilization of online resources further optimizes the learning process, allowing for targeted practice and immediate feedback.The benefits of using practice tests and review materials are undeniable. Practice tests simulate the actual exam environment, allowing students to familiarize themselves with the format, question types, and time constraints.
This reduces test anxiety and improves time management skills. Review materials, such as textbooks, workbooks, and online tutorials, provide comprehensive coverage of key concepts and offer opportunities for repeated practice and reinforcement of learned material. Consistent engagement with these resources strengthens conceptual understanding and builds problem-solving proficiency. The more exposure a student has to diverse problem types, the better equipped they will be to handle unexpected challenges on the actual exam.
Effective Use of Online Resources for Algebra 1 Practice
Online resources offer a wealth of Algebra 1 practice materials. Students should prioritize websites and platforms offering structured lessons, interactive exercises, and immediate feedback. Khan Academy, for example, provides a comprehensive library of Algebra 1 videos, practice problems, and personalized learning paths. Other platforms, like IXL and Mathway, offer targeted practice exercises categorized by topic and difficulty level.
Effective utilization involves focusing on areas where the student struggles, using the resources to address knowledge gaps, and regularly reviewing completed work to identify recurring errors. It’s crucial to avoid simply passively consuming the material; active engagement, including taking notes and working through problems independently before checking answers, is essential for effective learning.
Helpful Resources for Additional Practice
A variety of resources can supplement classroom learning and enhance Algebra 1 Regents exam preparation. These resources offer diverse approaches to learning and provide opportunities for targeted practice.Textbooks and workbooks: These provide a structured approach to learning Algebra 1 concepts and offer numerous practice problems. Choosing a reputable textbook aligned with the New York State curriculum is crucial.Online platforms: Websites like Khan Academy, IXL, and Mathway offer interactive exercises, video tutorials, and personalized learning paths.
These platforms allow for targeted practice and immediate feedback.Past Regents exams: Practicing with past Regents exams is invaluable for familiarizing oneself with the exam format and question types. The New York State Education Department website provides access to these exams and their answer keys.Tutoring and study groups: Working with a tutor or participating in a study group can provide personalized support and facilitate collaborative learning.
Explaining concepts to others reinforces understanding and helps identify areas needing further attention.
Consistent practice and targeted review are key to success on the Algebra 1 Regents exam.
Understanding the Scoring System for the Algebra 1 Regents Exam
The Algebra 1 Regents Exam scoring system is crucial for understanding your performance and identifying areas for improvement. A thorough understanding of the scoring rubric and conversion process is essential for effective exam preparation and post-exam analysis. This section details the scoring system, providing examples and explanations to clarify the process.
Scoring Rubric Details
The Algebra 1 Regents Exam typically uses a combination of multiple-choice, short-answer, and problem-solving questions. Each question type is assigned a specific point value, contributing to the overall raw score. Partial credit is often awarded for short-answer and problem-solving questions, depending on the correctness and completeness of the response. The precise point allocation may vary slightly from year to year, so consulting the official scoring guide for the specific exam year is recommended.
| Question Type | Points per Question | Total Possible Points (Example) | Partial Credit |
|---|---|---|---|
| Multiple Choice | 1 | 24 | No |
| Short Answer | 2-3 | 36 | Yes |
| Problem-Solving | 4-6 | 40 | Yes |
| Total | 100 |
Short-answer questions are assessed based on the accuracy and completeness of the answer. A complete answer demonstrates a clear understanding of the underlying concepts and procedures. An incomplete answer might show some understanding but lack crucial steps or explanations. For example, correctly finding the solution to an equation but omitting the steps to arrive at that solution would likely result in partial credit.
Incorrect answers receive no credit. Problem-solving questions require a demonstration of the problem-solving process, including showing all work and providing a clear, justified solution. Partial credit is awarded based on the correctness of individual steps and the overall approach.
Raw Score Conversion to Final Grades
The raw score (total points earned) is converted to a final grade using a predetermined formula. This formula might involve scaling or weighting factors to adjust for variations in exam difficulty across different administrations. The precise formula is not publicly released but is generally a linear transformation.
The general formula might be represented as: Final Grade = a
Raw Score + b, where ‘a’ and ‘b’ are constants determined by the New York State Education Department.
The specific conversion table varies from year to year, but a sample is shown below:
| Raw Score Range | Final Grade (Example) |
|---|---|
| 90-100 | A |
| 80-89 | B |
| 70-79 | C |
| 60-69 | D |
| 0-59 | F |
Score Interpretations and Examples
Example 1 (Multiple Choice): Correctly identifying the slope of a linear equation receives 1 point. An incorrect answer receives 0 points.Example 2 (Short Answer): Solving a system of equations correctly with all steps shown earns full credit (e.g., 2 points). Showing the correct method but making a minor arithmetic error might earn partial credit (e.g., 1 point). An incorrect method with an incorrect answer receives 0 points.Example 3 (Problem-Solving): Correctly solving a word problem involving quadratic equations, showing all work and a clear explanation, earns full credit (e.g., 4 points).
Missing a crucial step or making a significant error in the process might earn partial credit (e.g., 2 points). An incorrect solution with no supporting work receives 0 points.Computational errors reduce the score based on the severity of the error and its impact on the final answer. Conceptual errors, where the student misunderstands the underlying mathematical principles, result in more significant point deductions.
Procedural errors, such as incorrect application of formulas or methods, lead to partial credit or no credit depending on the extent of the error.A high score (e.g., 95) indicates strong mastery of Algebra 1 concepts and skills. An average score (e.g., 75) suggests a moderate understanding with some areas needing improvement. A low score (e.g., 50) indicates significant gaps in understanding and requires focused remediation.
Additional Considerations
There are no penalties for incorrect answers on the Algebra 1 Regents Exam. Ambiguous answers are handled by the scorers using professional judgment and the provided scoring rubric. A score review or appeal process is available, but it involves specific procedures and timelines Artikeld by the New York State Education Department. These procedures usually involve submitting a formal request within a specified timeframe and providing supporting documentation.
Common Mistakes to Avoid
Success on the Algebra 1 Regents exam hinges not only on understanding the concepts but also on avoiding common pitfalls. Many students possess the necessary knowledge but lose points due to careless errors or misunderstandings of specific question types. This section will highlight these frequent mistakes and provide strategies for preventing them.Many errors stem from a lack of careful attention to detail or insufficient practice applying learned concepts to diverse problem scenarios.
Consistent practice, coupled with a focused approach to problem-solving, is key to minimizing these mistakes. By actively identifying your weaknesses and focusing your study efforts, you can significantly improve your performance and achieve a higher score.
Algebraic Errors
Algebraic manipulation forms the core of the Algebra 1 Regents exam. Errors in this area often lead to incorrect solutions, even if the underlying concepts are understood. These mistakes frequently involve incorrect application of the order of operations (PEMDAS/BODMAS), improper handling of negative numbers, and mistakes in simplifying expressions.
- Incorrectly applying the order of operations (PEMDAS/BODMAS): For example, failing to address parentheses or exponents before multiplication or addition. This leads to incorrect simplification of expressions like 2 + 3 × 4, where the correct answer is 14, but incorrectly applying the order of operations may lead to 20.
- Errors involving negative numbers: Issues often arise with subtracting negative numbers, multiplying or dividing negative numbers, and simplifying expressions with multiple negative signs. For instance, incorrectly simplifying -( -5) as -5 instead of 5.
- Incorrect simplification of algebraic expressions: This encompasses mistakes in combining like terms, distributing negative signs, and factoring. A common error involves incorrectly distributing a negative sign across multiple terms within parentheses.
Equation Solving Errors
Solving equations is another crucial area where many students make mistakes. These errors often involve incorrect manipulation of equations, leading to inaccurate solutions.
- Incorrect application of inverse operations: Failing to perform the same operation on both sides of an equation is a common error, leading to an incorrect solution. For example, subtracting 5 from only one side of the equation x + 5 = 10.
- Errors in solving multi-step equations: Students may struggle with equations involving fractions, decimals, or variables on both sides. A frequent mistake is incorrectly isolating the variable.
- Mistakes in solving systems of equations: Errors often occur when using substitution or elimination methods, especially when dealing with complex equations or fractions.
Word Problem Interpretation Errors
Translating word problems into algebraic equations is a significant challenge for many students. Misinterpreting the problem statement can lead to incorrect equations and solutions.
- Incorrectly translating word problems into algebraic expressions or equations: This is often caused by misinterpreting the relationships described in the problem. For example, mistaking “more than” for “less than” in a problem involving addition or subtraction.
- Failing to define variables clearly: Without clearly defining variables, it’s easy to lose track of their meaning and create an incorrect equation.
- Not checking the reasonableness of the solution: After solving a word problem, it is crucial to check if the answer makes sense within the context of the problem. For instance, a negative solution for a problem involving length is clearly unreasonable.
Preparing for Different Question Types

Mastering the Algebra 1 Regents exam requires a strategic approach to each question type. Understanding the nuances of multiple-choice, short-answer, and free-response questions is crucial for maximizing your score. This section details effective strategies for tackling each question type, emphasizing efficient problem-solving and clear communication.
Multiple-Choice Question Strategies
Success with multiple-choice questions hinges on efficient elimination of incorrect options and a precise understanding of the question’s core meaning. Rushing through these questions often leads to careless errors.
Process of Elimination
The process of elimination is a powerful tool for narrowing down options and increasing your chances of selecting the correct answer. Begin by identifying and eliminating obviously incorrect answers. Common distractors include options that are close but not quite right, completely irrelevant to the problem, or based on common misconceptions.For example, consider this question: Solve for x: 2x + 5 = 11. (a) 8 (b) 3 (c) 6 (d) 16.
We can quickly eliminate (a) and (d) because they are far too large. Solving the equation, 2x = 6, yields x = 3, confirming (b) as the correct answer.
Analyzing Stems and Options
Carefully analyze the question stem (the main part of the question) to fully grasp what is being asked. Identify s and phrases that provide crucial clues. Different question stems require different approaches. For instance, questions asking for the “best” or “most likely” answer require a nuanced understanding of the context. Questions requiring calculations need a clear understanding of the steps and formulas involved.
Predicting Answers Before Reviewing Options
Before looking at the provided options, try to solve the problem independently. This prevents being swayed by cleverly worded distractors. For example, if the question asks for the slope of a line given two points, calculate the slope first; then compare your answer to the given options. This independent calculation provides a solid foundation for your choice and reduces the likelihood of selecting a distractor.
Short-Answer and Free-Response Question Strategies
Short-answer and free-response questions assess not only your mathematical knowledge but also your ability to clearly communicate your reasoning. A structured approach is essential for success.
Short-Answer Strategies
Answer short-answer questions concisely and precisely, using s and avoiding unnecessary details. Focus on providing the correct answer with minimal explanation. For example, if asked to state the Pythagorean Theorem, a succinct response like “a² + b² = c²” is sufficient. An ineffective response might include irrelevant information or rambling explanations.
Free-Response Strategies
Free-response questions require a well-structured and organized answer. Begin by outlining your response, planning the key points you will cover. Structure your answer with a clear introduction stating your approach, body paragraphs elaborating on your reasoning, and a concise conclusion summarizing your findings. For example, a free-response question asking to explain the process of solving a system of equations should include an introduction outlining the method (e.g., substitution or elimination), body paragraphs showing the step-by-step solution, and a conclusion stating the solution.
Examples Illustrating Different Approaches
| Question Type | Strategy | Example Question | Example Answer/Approach |
|---|---|---|---|
| Multiple Choice | Process of Elimination | Which of the following is a prime number? (a) 9 (b) 15 (c) 17 (d) 25 | Eliminate (a), (b), and (d) as they are composite numbers; (c) is the correct answer. |
| Multiple Choice | Analyzing Stems and Options | What is the x-intercept of the line y = 2x + 4? (a) 2 (b) 4 (c) -2 (d) -4 | The x-intercept occurs when y = 0; solving 0 = 2x + 4 gives x = -2; thus (c) is correct. |
| Short Answer | Use and Conciseness | Define a linear equation. | An equation whose graph is a straight line. |
| Free Response | Structured Answer | Solve the quadratic equation x²
| (Requires a structured answer showing the factoring process, finding the roots, and stating the solution.) |
Reviewing and Analyzing Past Exams

Past Regents exams are invaluable resources for Algebra 1 preparation. Analyzing them effectively allows for targeted study, strengthening weaknesses, and ultimately improving performance on the actual exam. This process goes beyond simply completing practice problems; it’s about understanding the exam’s structure, question types, and common pitfalls.Successfully navigating the Algebra 1 Regents exam requires a strategic approach to practice.
Reviewing past exams isn’t merely about solving problems; it’s a diagnostic tool revealing areas needing improvement. A methodical analysis allows for focused review, leading to significant score enhancement.
Identifying Areas of Weakness
Thoroughly reviewing past Regents exams involves more than just checking answers. After completing a practice exam, meticulously analyze each question, regardless of whether you answered it correctly or incorrectly. For incorrectly answered questions, identify the specific concept or skill you struggled with. For correctly answered questions, assess whether your solution was efficient and accurate, or if there were any areas for improvement in your problem-solving approach.
Categorize your errors; are they consistently in a specific area like quadratic equations or inequalities? This detailed analysis provides a clear picture of your strengths and weaknesses. For example, if you consistently miss questions involving word problems that require setting up equations, you know that this area needs focused attention. Similarly, repeated mistakes in simplifying expressions indicate a need to review fundamental algebraic rules.
Designing a Targeted Review Plan
Once areas of weakness have been identified, create a targeted review plan. This plan should prioritize the topics where you struggled the most. Don’t simply reread the textbook; actively seek out additional practice problems focusing on those specific topics. Use online resources, supplementary workbooks, or even create your own practice problems based on the types of questions you found challenging.
For example, if your analysis reveals weakness in solving systems of equations, dedicate a significant portion of your study time to this topic. This might involve reviewing different solution methods (substitution, elimination, graphing), working through numerous practice problems, and seeking clarification from a teacher or tutor if needed. This targeted approach ensures efficient use of study time, focusing on the areas that will have the greatest impact on your overall score.
Remember to track your progress as you work through the targeted review. This helps monitor your understanding and identify areas that might still require further attention.
Common Queries
Where can I find free Algebra 1 Regents practice PDFs?
Many websites offer free practice resources; search online for “Algebra 1 Regents practice tests.” However, always check the source’s reliability.
How much time should I spend on each question type during the exam?
Allocate time proportionally to the points awarded per question type. Practice tests help you gauge your pacing.
What if I don’t understand a concept explained in the practice materials?
Seek clarification from teachers, tutors, or online resources. Don’t hesitate to ask for help!
Are there any specific calculator requirements for the exam?
Check the official New York State Education Department website for the most up-to-date information on permitted calculators.


